
I dati qui analizzati sono stati scaricati dal repository della Protezione civile. Tra i vari modelli matematici a disposizione per descrivere il fenomeno della diffusione dell’epidemia del coronavirus, uno dei più semplici coinvolge alcuni “compartimenti”. Il primo compartimento S contiene gli individui che non presentano il virus all’interno del loro corpo e che risultano quindi “suscettibili” di essere infettati. Da questo compartimento ciascun individuo può spostarsi nel secondo compartimento I dove ci sono invece gli individui che sono stati infettati. Da qui ciascun individuo può andare in un terzo compartimento M che contiene i soggetti che hanno sviluppato i sintomi della malattia, diagnosticata di conseguenza tramite test e che siano stati isolati, a casa, in ospedale o in terapia intensiva. Da questo compartimento, un individuo passerà nel quarto e ultimo compartimento R dove si trovano gli individui guariti e quelli morti. Assumiamo qui che i guariti non contengano più il virus, o che comunque non possano trasmetterlo ad altri individui infettandoli. È comunque stato riportato che in Cina circa il 14% dei pazienti guariti dall’infezione da coronavirus presentano il virus nelle feci dopo due settimane dalla dimissione. Osserviamo che non tutti gli individui infetti passano nel compartimento M. Questo può accadere sia per una mancata o erronea diagnosi e/o isolamento. Più preoccupante è il caso in cui una frazione non trascurabile degli infetti non sviluppino i sintomi della malattia, pur potendo trasmetterla, cioè siano “portatori sani”. Questo sembra essere il caso per il coronavirus. Purtroppo, da circa la fine di febbraio non vengono più effettuati test diagnostici a campione sugli asintomatici che permetterebbero una stima della frazione dei portatori sani.
Consideriamo le quattro funzioni S(t), I(t), M (t) e R(t) che descrivono il numero di individui presenti al tempo t in ciascuno dei quattro compartimenti. A questo punto possiamo ragionare in termini deterministici considerando il flusso di spostamento da S ad I, quello da I ad M e quello da M ad R. Il primo flusso può essere assunto proporzionale sia al numero di individui suscettibili S(t) che al numero di infetti I(t). Gli altri due flussi possono invece essere assunti proporzionali ad I(t) e ad M(t) rispettivamente. Analogamente, possiamo ragionare in modo probabilistico rimpiazzando i flussi con delle probabilità. Nel caso deterministico, le tre funzioni possono essere determinate risolvendo numericamente un sistema di equazioni differenziali ordinario. Nel caso stocastico possiamo usare invece l’algoritmo di simulazione di Gillespie.
Ci siamo finora focalizzati sul numero C(t) = M (t) + R(t) di persone che sono state contagiate ed osservate fino al tempo t. Abbiamo optato per questa scelta sperando che gli errori da cui sono affette le misure delle singole variabili, e.g. il numero dei morti, di cui C(t) è la somma, si compensino. La funzione C(t) è per definizione crescente nel tempo, o meglio non decrescente. Inoltre, dalle soluzioni ottenute numericamente, osserviamo un aumento progressivo del tasso di crescita di C(t) fino ad un massimo oltre il quale tale tasso diminuisce, mentre C(t) continua a crescere ma sempre più lentamente e dopo un tempo sufficientemente lungo non ha in pratica più variazioni. Una funzione che ha questo andamento è la funzione “logistica”
y 0 /(1 + exp(−(t − t 0 )/τ ))
come mostrato in figura 1. Dei tre parametri y 0 , t 0 e τ contenuti in questo modello, il parametro positivo τ influenza la velocità con cui viene raggiunto il valore limite: diminuendo il suo valore, aumenta tale velocità.
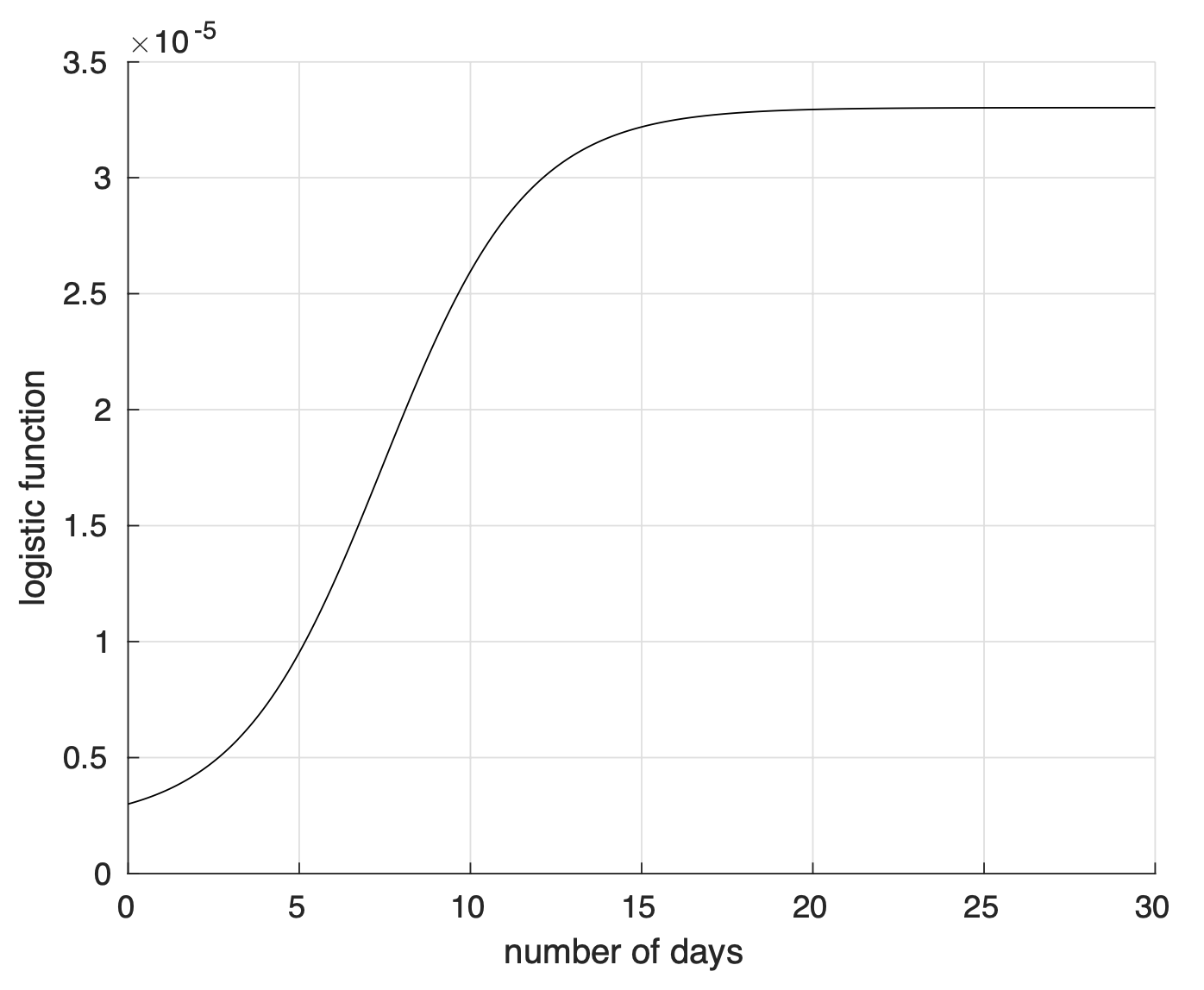
Figura 1. Esempio di andamento temporale di una variabile descritta da una funzione logistica.
In figura 2 si osserva la sequenza temporale della frazione dei contagiati osservati in Italia rispetto alla popolazione nazionale, assieme ad un fit con due modelli matematici applicati in sequenza in ciascuno di due sotto-intervalli contigui in cui abbiamo diviso l’intervallo temporale. Il modello utilizzato in ciascun sotto-intervallo è di tipo geometrico y02t/τ . Questa funzione, al contrario della logistica, cresce indefinitivamente e cosı̀ fa anche il suo tasso di crescita. Il parametro positivo τ rappresenta il tempo di raddoppio del valore della funzione. Più basso è il valore di questo parametro, più rapidamente cresce nel tempo il valore della funzione. La scelta di usare due modelli in sequenza è stata motivata dal cambiamento del criterio di identificazione dei contagiati avvenuto alla fine del mese di Febbraio, che non coinvolge più l’uso di tamponi su soggetti asintomatici. Sfortunatamente, si intuisce facilmente che la frazione dei contagiati effettivi dopo il cambio di criterio risulta significativamente sottostimata. Sulla base dei dati osservati fino a 12 Marzo alle 18, a livello dell’intera Italia non c’è evidenza di riduzione del tasso di crescita dei contagiati osservati. Infatti l’adattamento del modello ai dati è equivalente a quello in cui la funzione geometrica nel secondo sotto-intervallo è sostituita dalla logistica.
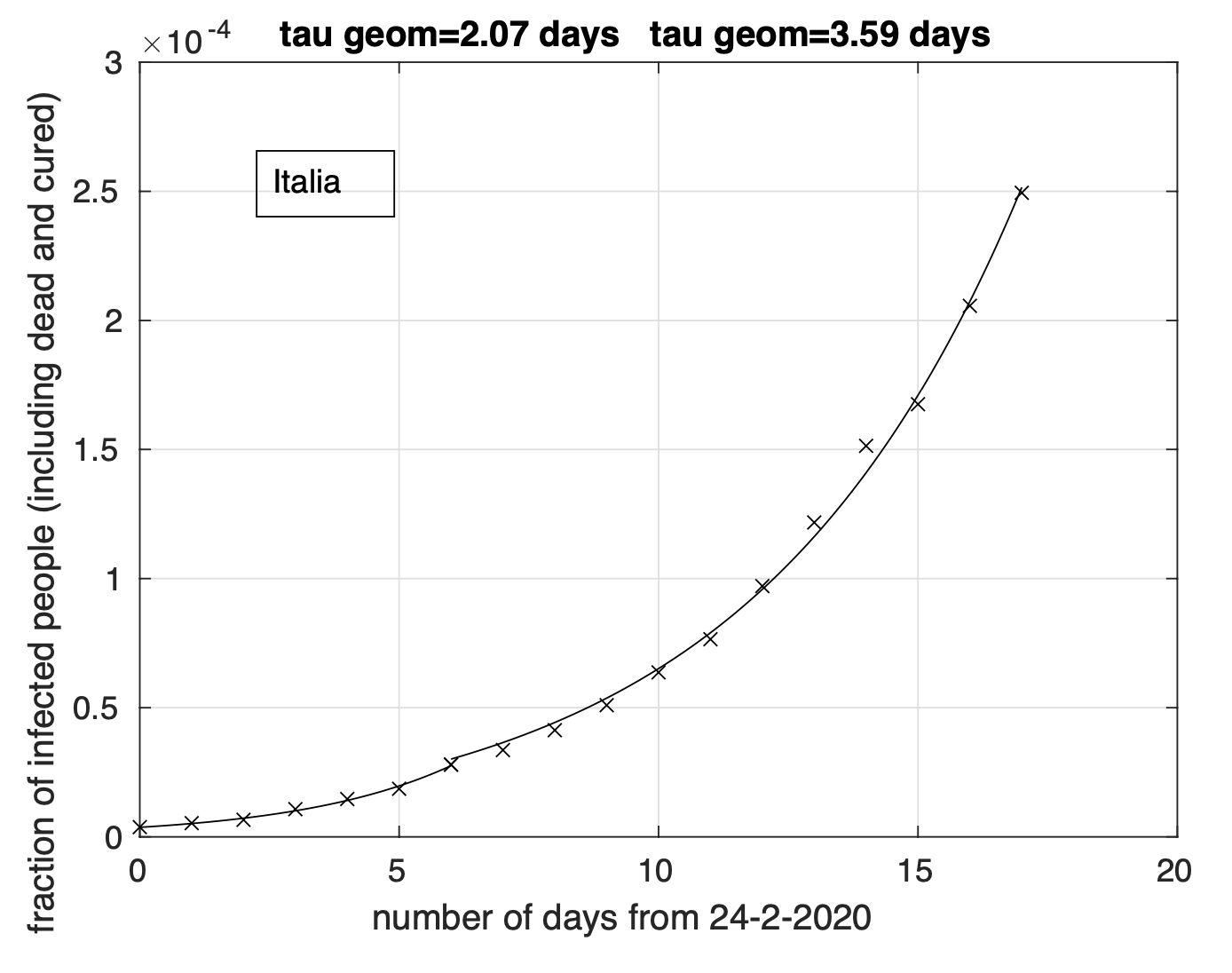
Figura 2. Sequenza della frazione del numero dei contagiati osservati in Italia rispetto alla popolazione nazionale. Il miglior fit con un modello doppio geometrico è sovrapposto ai dati.
Abbiamo considerato le sequenze temporali dal 1 marzo della frequenza dei contagiati osservati rispetto alla popolazione regionale delle nove regioni più colpite del “nord”: Lombardia, Emilia, Veneto, Marche, Piemonte, Toscana, Liguria, Trentino e Friuli. Sulla base di questi dati, abbiamo raggruppato le nove regioni in tre gruppi ciascuno composto da sequenze “simili”. A questo scopo abbiamo utilizzato l’algoritmo di clustering gerarchico che minimizza localmente la somma delle variazioni dei dati all’interno di ciascun gruppo. Nella Figura 3 viene mostrato il cosiddetto “dendrogramma”, cioè l’albero che visualizza i successivi raggruppamenti dell’algoritmo. Si parte dal livello più basso, dove ciascuna delle nove sequenze costituisce un gruppo sino ad arrivare al livello più alto, dove tutte e nove le sequenze sono in un unico gruppo. Il dendrogramma mostra chiara evidenza della presenza di tre gruppi:
- Lombardia;
- Emilia, Veneto e Marche;
- Piemonte, Toscana, Liguria, Trentino e Friuli.
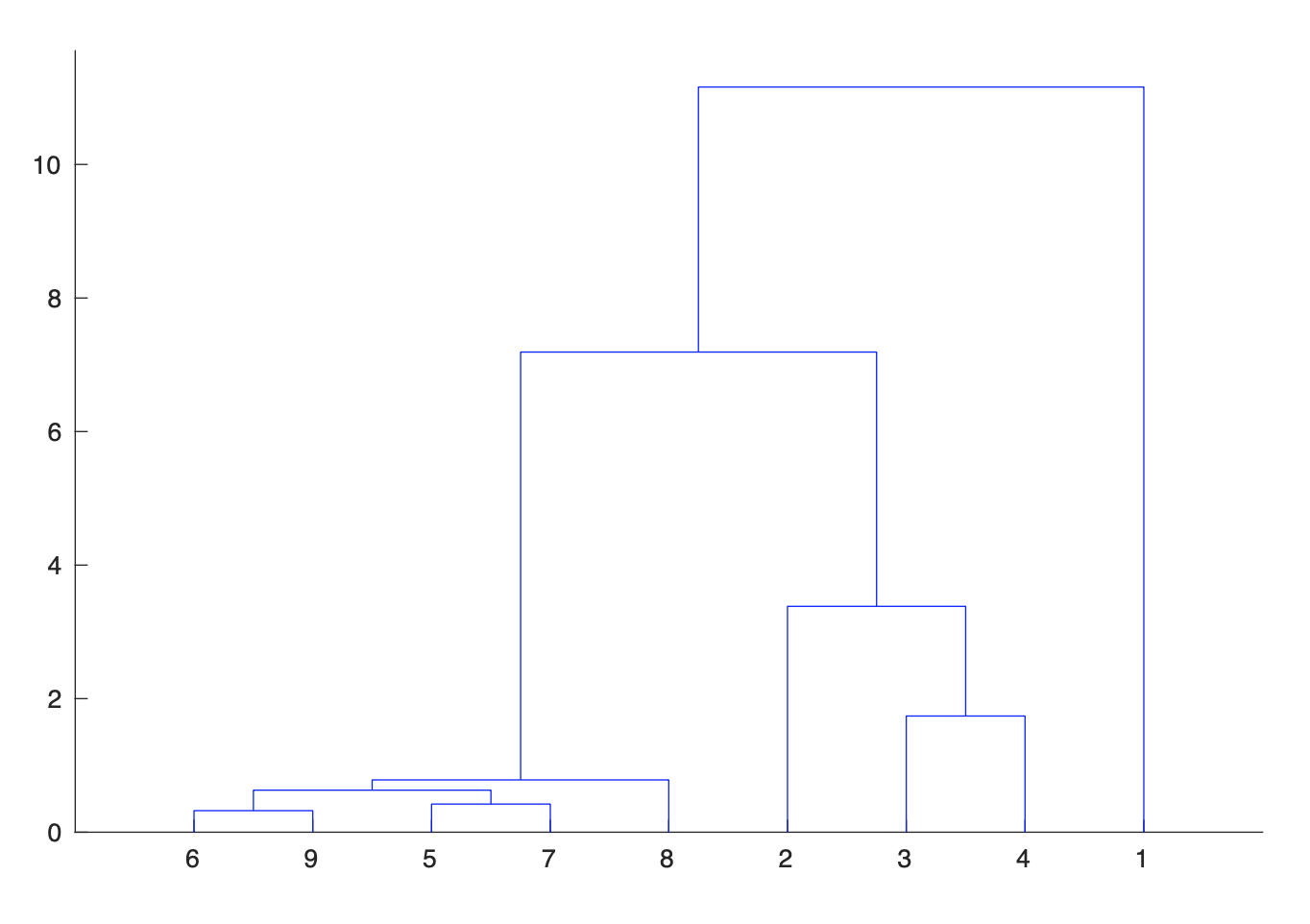
Figura 3. Dendrogramma per il raggruppamento delle nove regioni considerate tramite l’algoritmo di clustering gerarchico applicato alle nove sequenze delle frazioni dei contagiati osservati a partire dal 1 Marzo.
Per la Lombardia non si osserva evidenza di diminuzione del tasso di crescita della frazione dei contagiati osservati che segue un modello doppio esponenziale, come si può apprezzare in Figura 4 ed in Figura 5 a partire dal 1 marzo in scala semi-logaritmica, per cui la funzione esponenziale diventa una retta. Le sequenze relative alle regioni nel secondo gruppo mostrano evidenza di diminuzione del tasso di crescita. Infatti il modello logistico si adatta meglio ai dati di quello geometrico.

Figura 4. Sequenza della frazione dei contagiati osservati in Lombardia rispetto alla popolazione della regione. Il miglior fit con un modello doppio geometrico è sovrapposto ai dati.
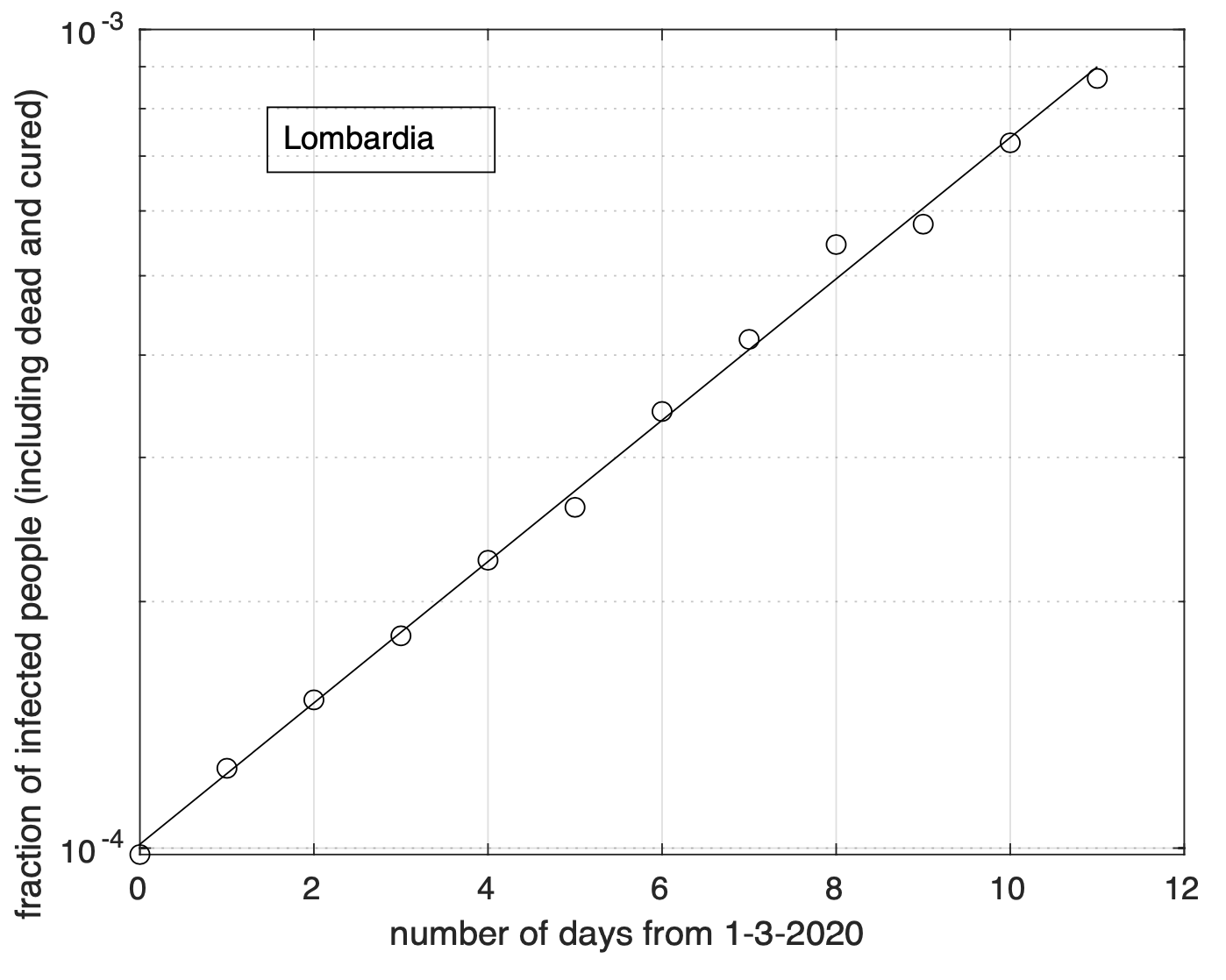
Figura 5. Come nella Figura 4, ma per i dati a partire dal 1 Marzo ed in scala semi-logaritmica. La linea retta rappresenta il modello esponenziale stimato a partire dai dati.
In Figura 6 possiamo osservare il risultato relativo all’Emilia. Questo è più evidente per le regioni del terzo gruppo, come ad esempio nel caso del Piemonte, illustrato in Figura 7.
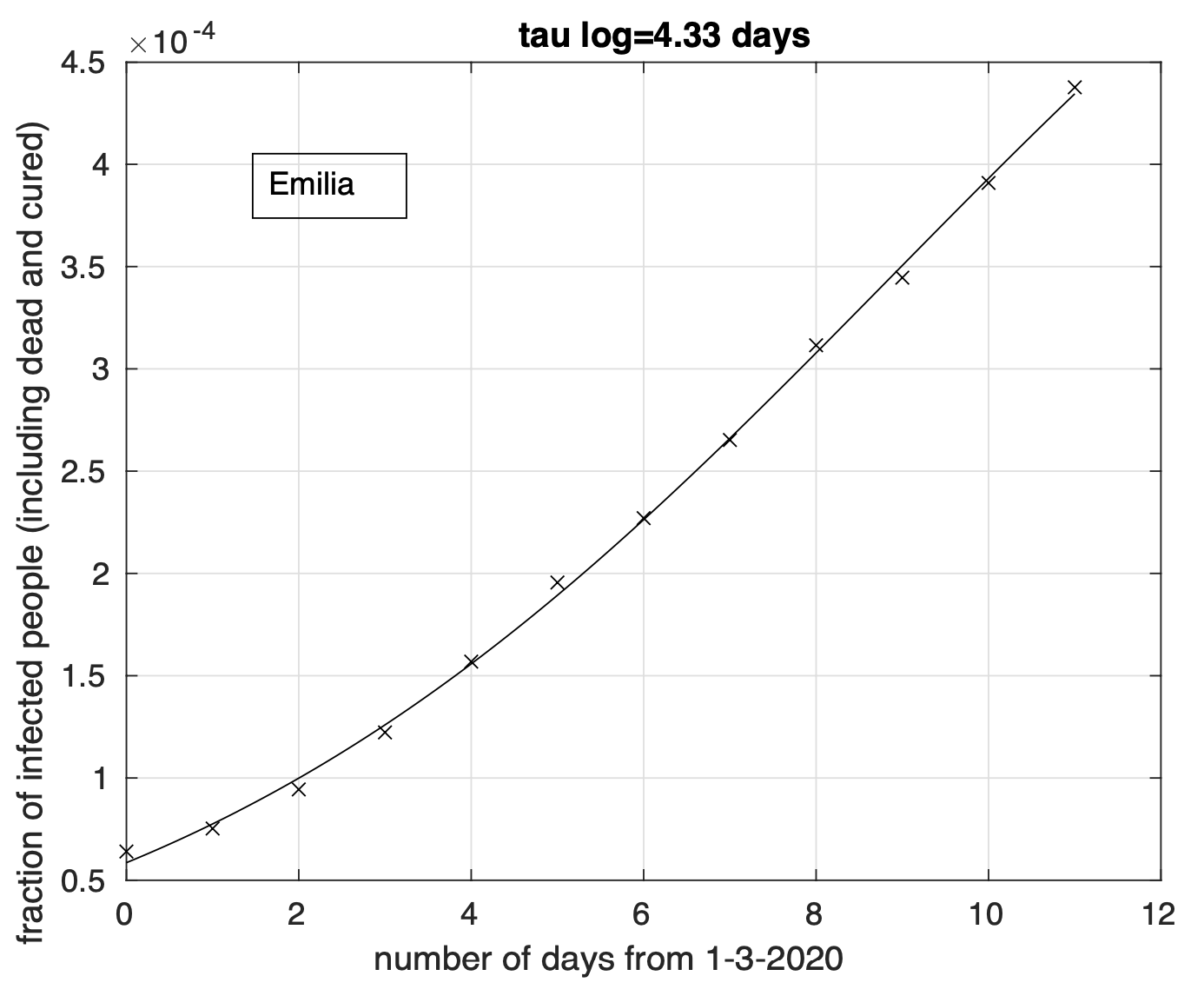
Figura 6. Sequenza della frazione dei contagiati osservati in Emilia rispetto alla popolazione della regione. Il miglior fit con un modello logistico è sovrapposto ai dati.
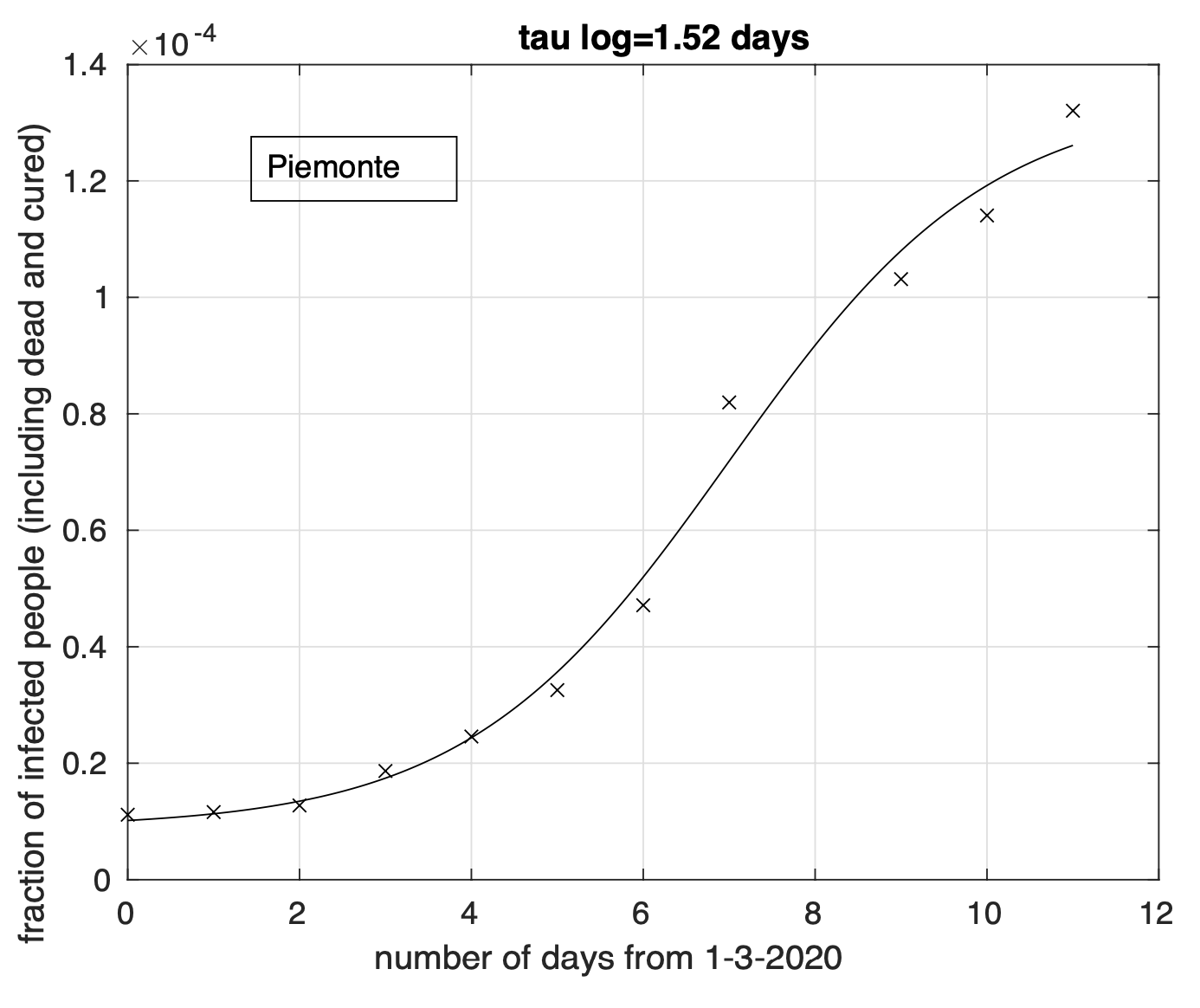
Figura 7. Sequenza della frazione dei contagiati osservati in Piemonte rispetto alla popolazione della regione. Il miglior fit con un modello misto geometrico-logistico è sovrapposto
ai dati.
I valori stimati del tempo dal 1 Marzo a partire dal quale non si avranno praticamente variazioni della frazione dei contagiati osservati sono stati stimati separatamente per ciascuna delle otto regioni rimaste dopo aver escluso la Lombardia. Sulla base del raggruppamento effettuato, riportiamo il range per il gruppo Emilia, Veneto e Marche: 40-60 giorni e quello per il gruppo Piemonte, Toscana, Liguria, Trentino e Friuli: 20-30 giorni. La bontà della stima dei range è limitata dal ridotto intervallo temporale in cui il tasso di crescita diminuisce. Col tempo tale intervallo aumentarà e di conseguenza anche la bontà della stima. Naturalmente questo vale se non ci saranno variazioni significative del comportamento della popolazione in relazione ai meccanismi principali alla base del fenomeno di diffusione del virus. Infatti, l’analisi effettuata oggi ha messo in evidenza un aumento del tasso di crescita a partire dal 10-11 Marzo che segue una sua precedente diminuzione per le sequenze di Sicilia (vedi Figura 8) e Lazio e meno marcatamente per la Puglia. È possibile che questo sia stato causato dall’esodo dal nord al sud avvenuto in seguito al decreto che l’8 marzo istituiva la zona rossa in Lombardia.
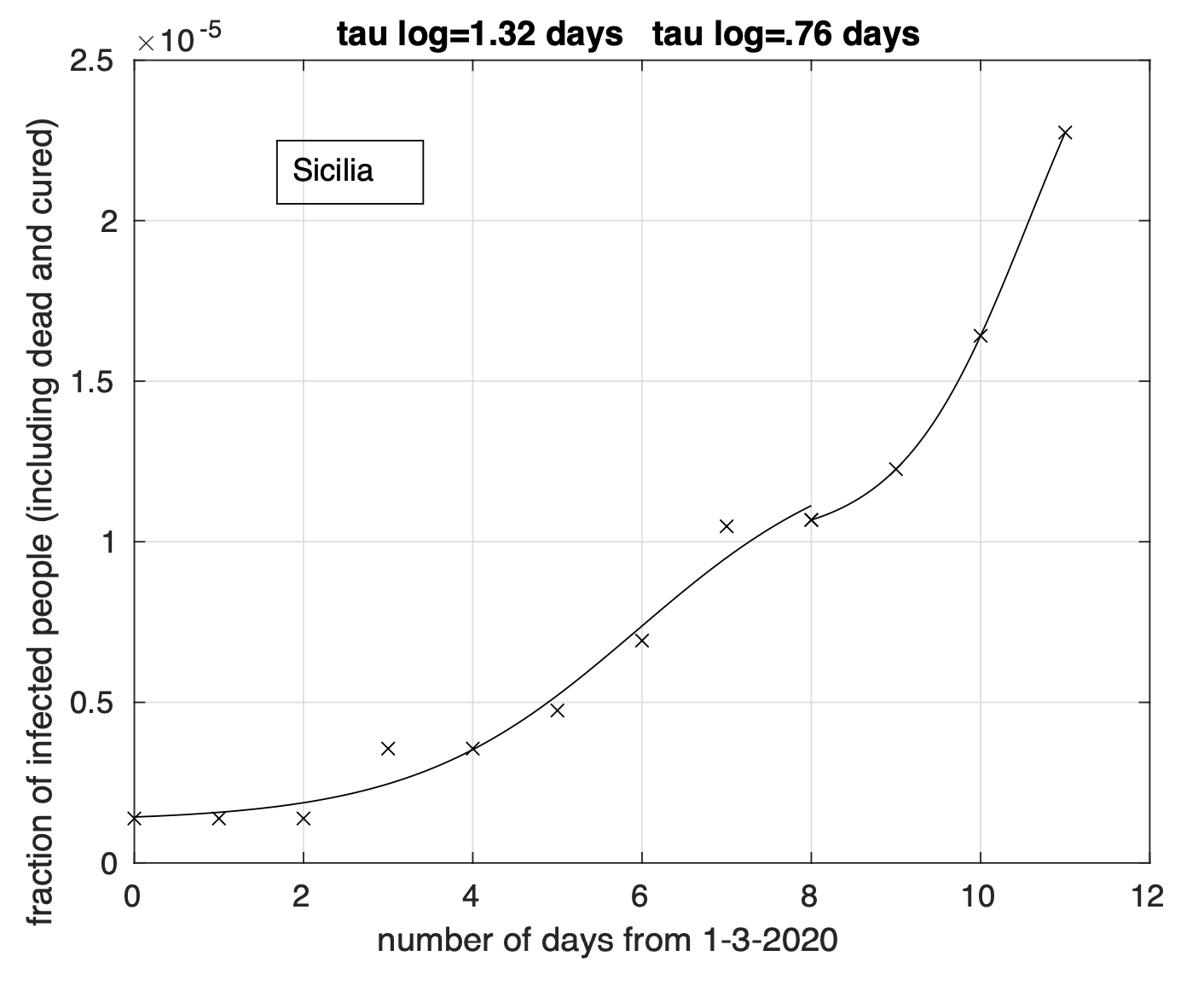
Figura 8. Sequenza della frazione dei contagiati osservati in Sicilia rispetto alla popolazione della regione. Il miglior fit con un modello doppio logistico è sovrapposto ai dati.
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche

