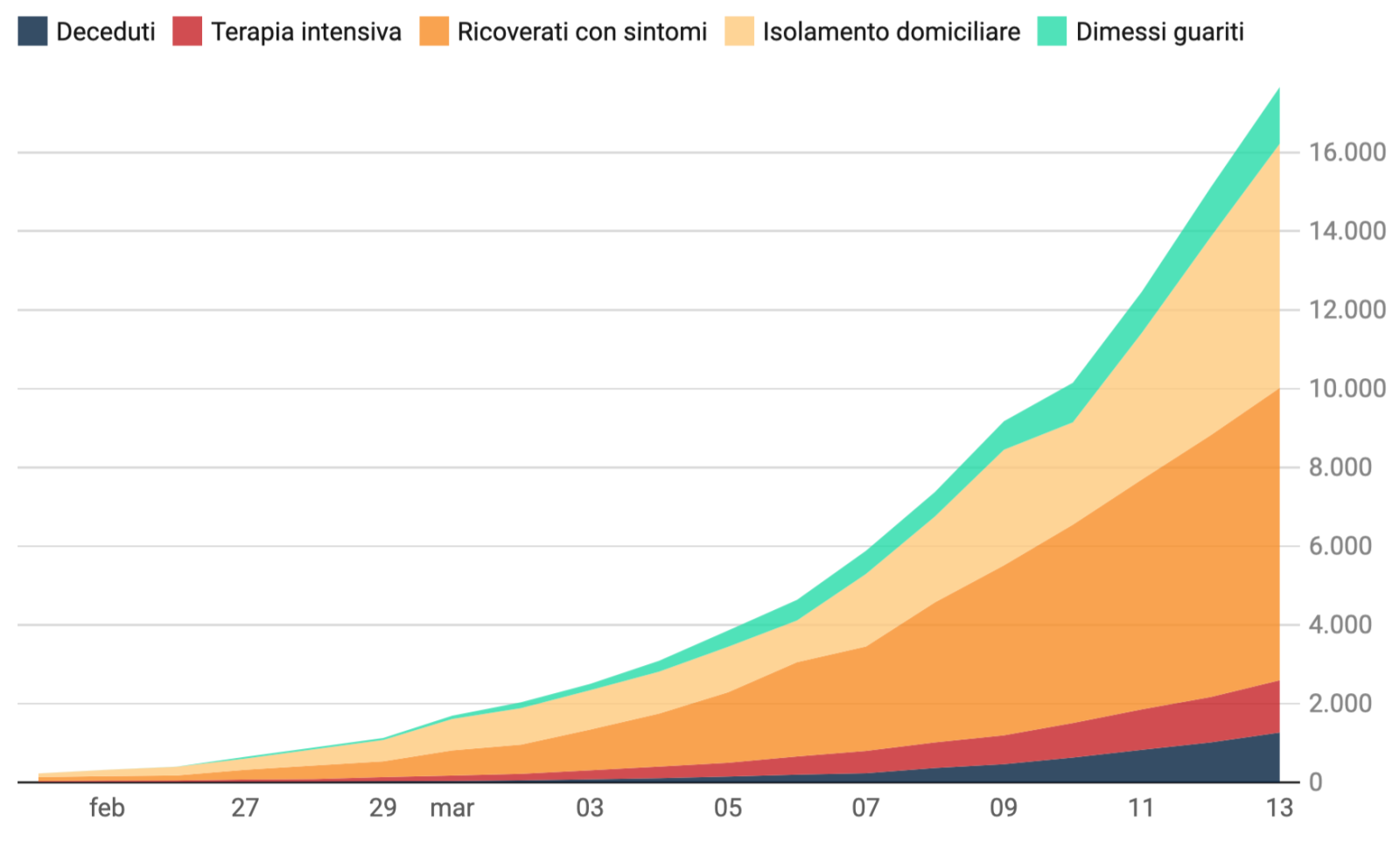
Illustriamo qui i risultati relativi all’analisi a livello regionale e delle sei province della Lombardia al momento maggiormente colpite dei dati aggiornati alle 18 del 13 marzo 2020, che sostituiscono o integrano quelli nel documento del 12 marzo. I dati a livello regionale sono stati scaricati dal sito https://github.com/pcm-dpc/COVID-19 e quelli a livello provinciale dal sito https://github. com/pcm-dpc/COVID-19/tree/master/dati-province.
Per quanto riguarda la Lombardia, osserviamo una riduzione del tasso di crescita della frazione dei contagiati osservati relativa ai giorni 12-13 marzo, come si può osservare in scala semi-logaritmica nella figura 1. Comunque, questo potrebbe essere dovuto ad un problema tecnico di conteggio, già accaduto il 10 marzo. Aspettiamo i prossimi giorni per una conferma della diminuzione del tasso.
Il range dei valori stimati del tempo dal 1 marzo a partire dal quale non si avranno praticamente variazioni della frazione dei contagiati osservati per il gruppo delle regioni Emilia, Veneto e Marche è 60-80 giorni. Per il gruppo delle regioni Toscana, Liguria e Trentino il range dei valori stimati è invece 20-40 giorni. Le altre due regioni del terzo gruppo dell’analisi del 12 marzo, Piemonte e Friuli, presentano un aumento del tasso di crescita relativo ai giorni 12-13 marzo, per cui sono state escluse dall’analisi col modello logistico. I prossimi giorni chiariranno la situazione.
Per quanto riguarda l’aumento del tasso di crescita a partire dall’11 marzo che segue una sua precedente diminuzione osservato precedentemente per le sequenze di Sicilia e Lazio e meno marcatamente per la Puglia è stato osservato anche nelle altre tre regioni con numero dei contagiati osservati maggiore di 50 per le quali abbiamo ora effettuato l’analisi: Campania, Abruzzo ed Umbria. In figura 2 vediamo la sequenza della frazione dei contagiati osservati cumulati in queste sei regioni rispetto alla somma delle loro popolazioni. Questo andamento è visibile in ciascuna delle sei regioni. Come già anticipato nel documento precedente, è possibile che questo aumento del tasso di crescita sia stato causato dall’esodo dal nord al sud avvenuto in seguito al decreto che l’8 marzo istituiva la zona rossa in Lombardia. Anche il fenomeno dell’assalto ai supermercati potrebbe avere delle ripercussioni nella diffusione dell’epidemia.
Abbiamo inoltre effettuato l’analisi dei dati delle sei province della Lombardia attualmente maggiormente colpite: Bergamo, Brescia, Cremona, Lodi, Milano e Pavia. Per i giorni considerati, dal 1 marzo al 13 marzo, rimangono alcune centinaia di casi della Lombardia (ma vale anche per altre regioni) che nel database non sono ancora assegnati a nessuna delle sue province. Abbiamo ignorato tali casi. L’analisi per le province di Brescia, Cremona e Lodi (vedi figure 3, 4 e 5) mette in evidenza una diminuzione del tasso di crescita, in particolare per quella di Lodi, forse a causa del suo miglior isolamento. Infatti l’adattamento ai dati del modello logistico è migliore che per il modello geometrico. Per la provincia di Pavia, (vedi Figura 6) l’adattamento dei due modelli è lo stesso. Per le restanti province di Bergamo e Milano (vedi Figure 7, 8), si ha un modesto miglior adattamento in corrispondenza del modello logistico.
In relazione al modello illustrato nel documento del 12 marzo, è utile sottolineare l’importanza della consistenza numerica dei portatori sani per la diffusione dell’epidemia. A supporto dell’ipotesi della presenza di una frazione non trascurabile di portatori sani nell’epidemia di coronavirus in Italia, c’è la ripetuta loro citazione, oltre a fattori demografici, da parte degli esperti delle istituzioni sanitarie nazionali per spiegare il significativo aumento del tasso di mortalità in Italia rispetto a quello in Cina. Infatti, ignorando il numero di portatori sani, il numero dei contagiati effettivi è sostituito dal più piccolo numero dei contagiati osservati. Questo diminuisce il denominatore nel calcolo della mortalità che risulterebbe in questo modo sovrastimata. Osserviamo che in questo contesto specifico, sono proprio i portatori sani i soggetti più rilevanti per la diffusione dell’epidemia. Infatti, i soggetti infettati che non sono portatori sani, sviluppano i sintomi in un tempo medio di 5 giorni circa, che sommato ad un tempo medio di diagnosi di 2 giorni, porta ad un tempo di una settimana circa in cui il soggetto può infettarne altri, essendo isolato in ospedale o a casa subito dopo la diagnosi. Un portatore sano invece, a meno che non abbia un ceto sociale elevato e sia sottoposto al test, non sa di esserlo e piò tranquillamente infettare altri soggetti. E quindi evidente l’importanza delle misure di limitazione della mobilità e più in generale quelle per la riduzione del rischio di infezione. Nel momento in cui il numero dei contagiati osservati rimarrà praticamente invariato, l’evoluzione dipenderà proprio dalla percentuale dei portatori sani. Se essa sarà non trascurabile, rimuovendo le misure di riduzione del rischio, sarà necessario lo sviluppo di una cura per evitare una ripartenza della diffusione e una decimazione selettiva, per età, della popolazione. Allo scopo di effettuare previsioni sulla diffusione dell’epidemia di coronavirus sulla base di modelli informativi, assieme a Marco Massa, dell’Imperial College, stiamo considerando un modello a compartimenti che tiene conto della presenza di portatori sani, il cui numero nel tempo costituisce una delle funzioni incognite. ll range dei valori stimati del tempo dal 1 marzo a partire dal quale non si avranno praticamente variazioni della frazione dei contagiati osservati per il gruppo delle province di Brescia, Cremona, Lodi, Bergamo e Milano è 30-50 giorni.
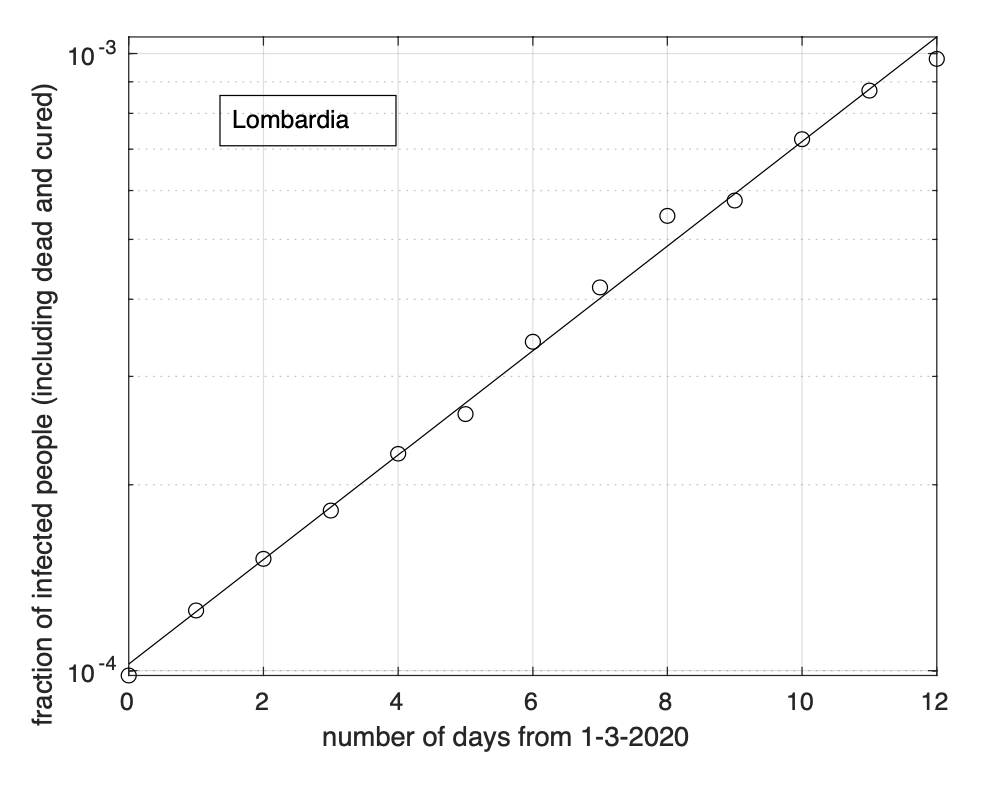
Figure 1: Frazione del numero di contagiati osservati in Lombardia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo ed in scala semi-logaritmica. La linea retta rappresenta il modello esponenziale stimato a partire dai dati. Notiamo un buon adattamento dei dati al modello teorico.
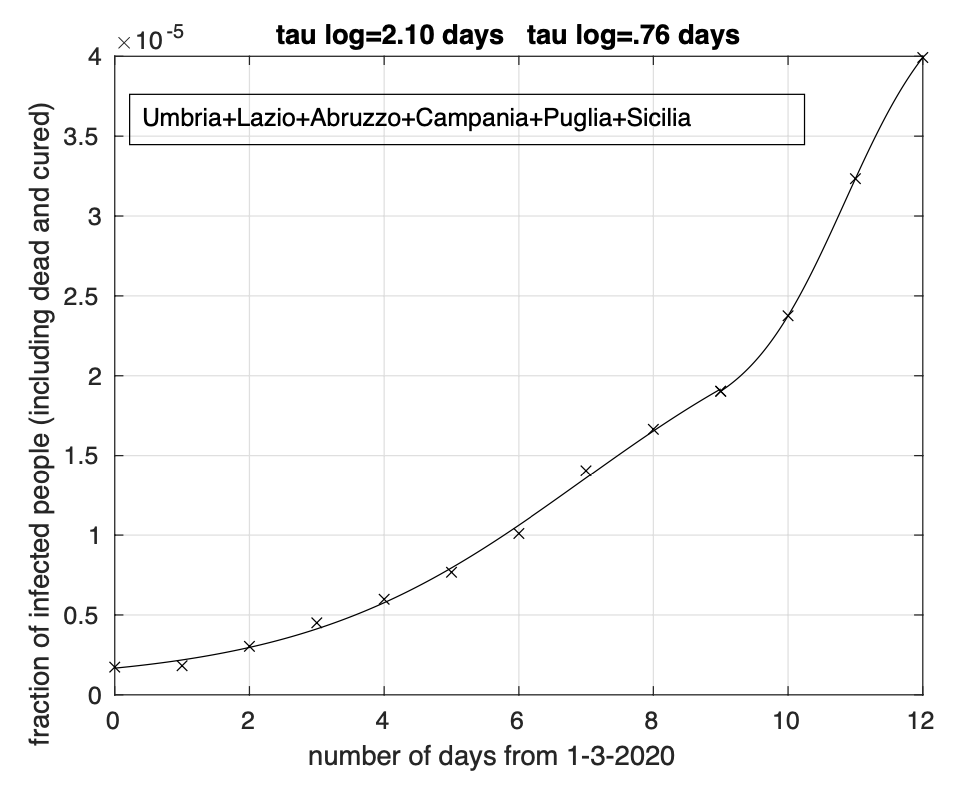
Figure 2: Sequenza della frazione dei contagiati osservati cumulati delle regioni Umbria, Lazio, Abruzzo, Campania, Puglia e Sicilia rispetto alla somma delle loro popolazioni. Il miglior fit con un modello doppio logistico è sovrapposto ai dati. Notiamo un aumento del tasso di crescita a partire dall’11 marzo dopo una sua precedente diminuzione.
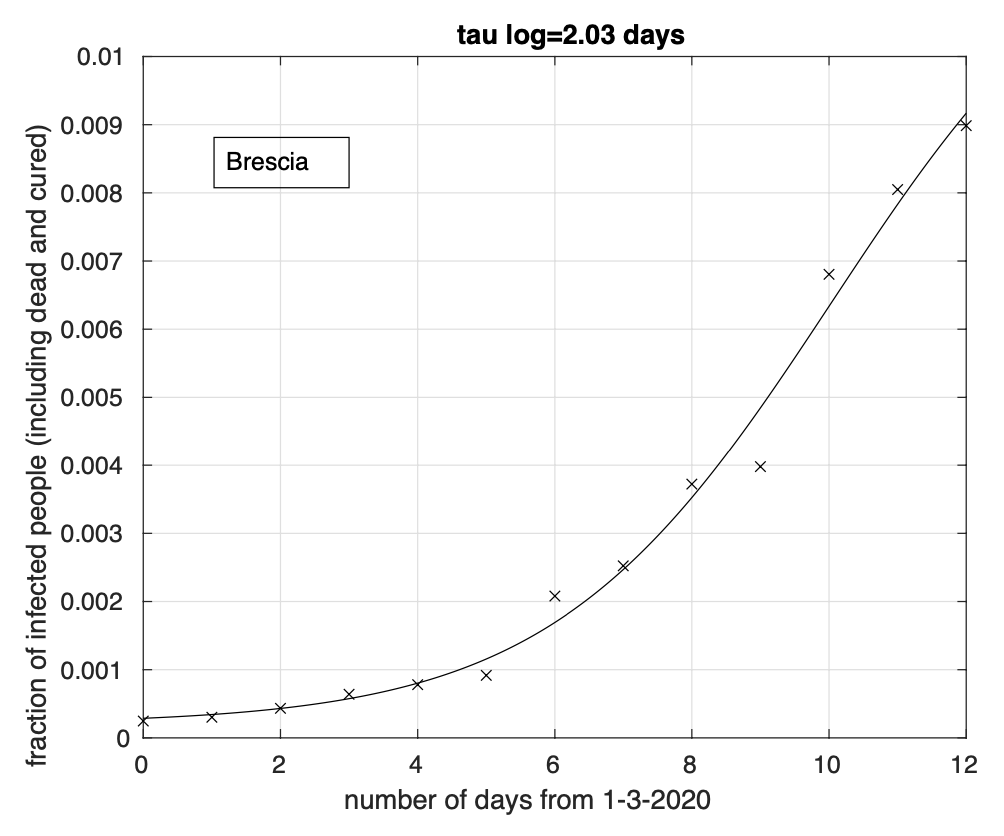
Figure 3: Sequenza della frazione dei contagiati osservati nella provincia di Brescia rispetto alla popolazione della provincia. Il miglior fit con un modello logistico è sovrapposto ai dati.
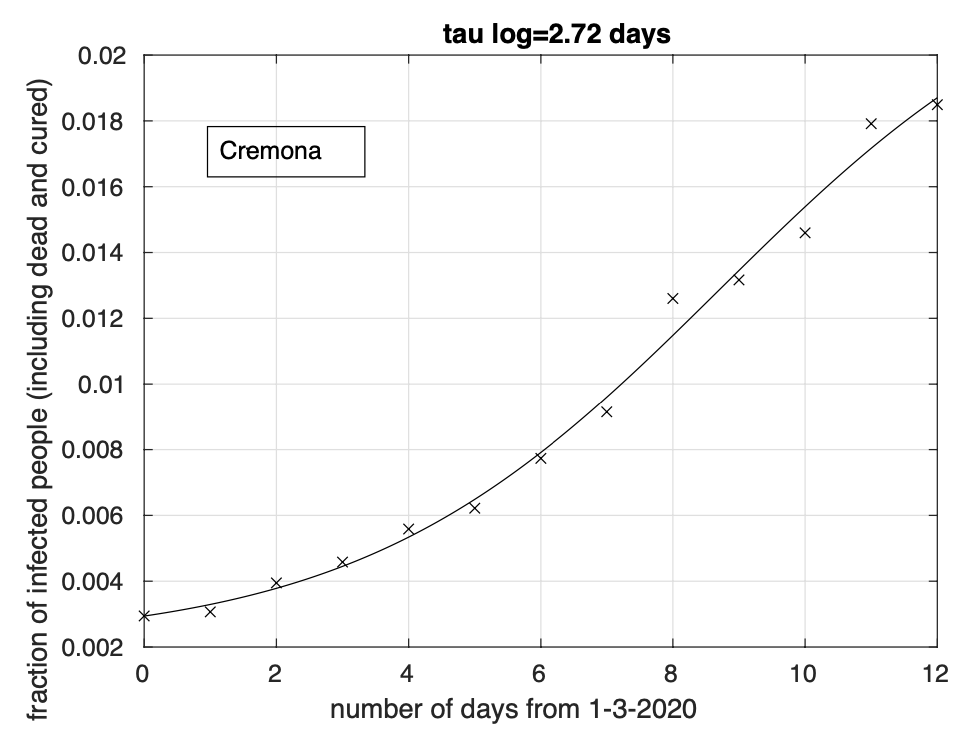
Figure 4: Sequenza della frazione dei contagiati osservati nella provincia di Cremona rispetto alla popolazione della provincia. Il miglior fit con un modello logistico è sovrapposto ai dati.
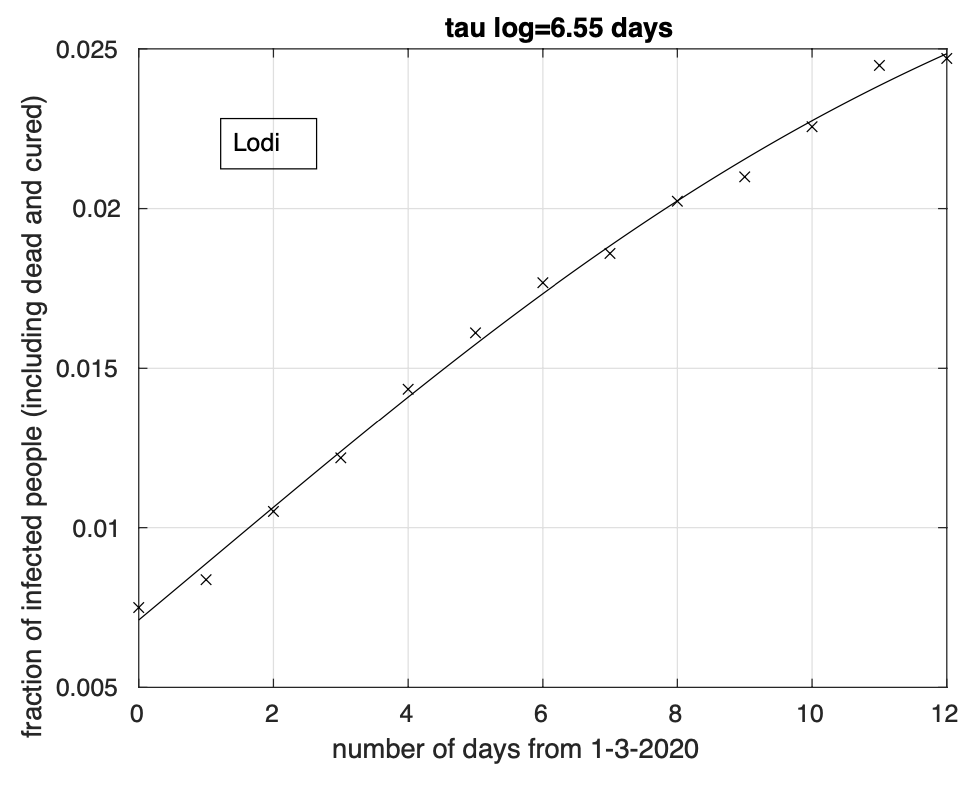
Figure 5: Sequenza della frazione dei contagiati osservati nella provincia di Lodi rispetto alla popolazione della provincia. Il miglior fit con un modello logistico è sovrapposto ai dati.
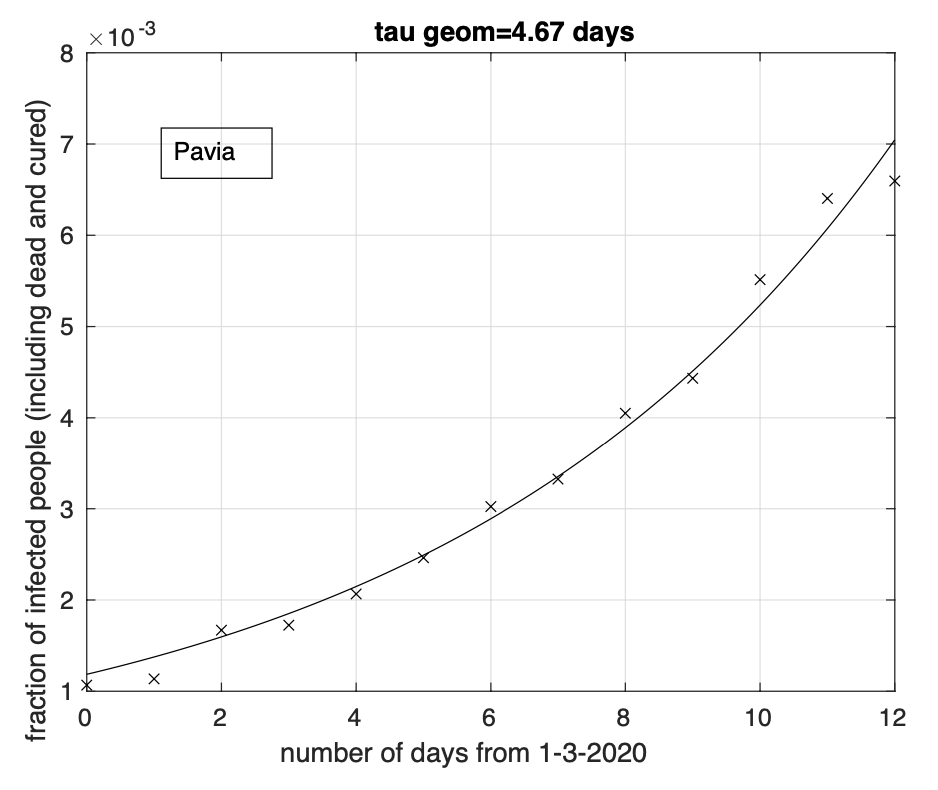
Figure 6: Sequenza della frazione dei contagiati osservati nella provincia di Pavia rispetto alla popolazione della provincia. Il miglior fit con un modello geometrico è sovrapposto ai dati.
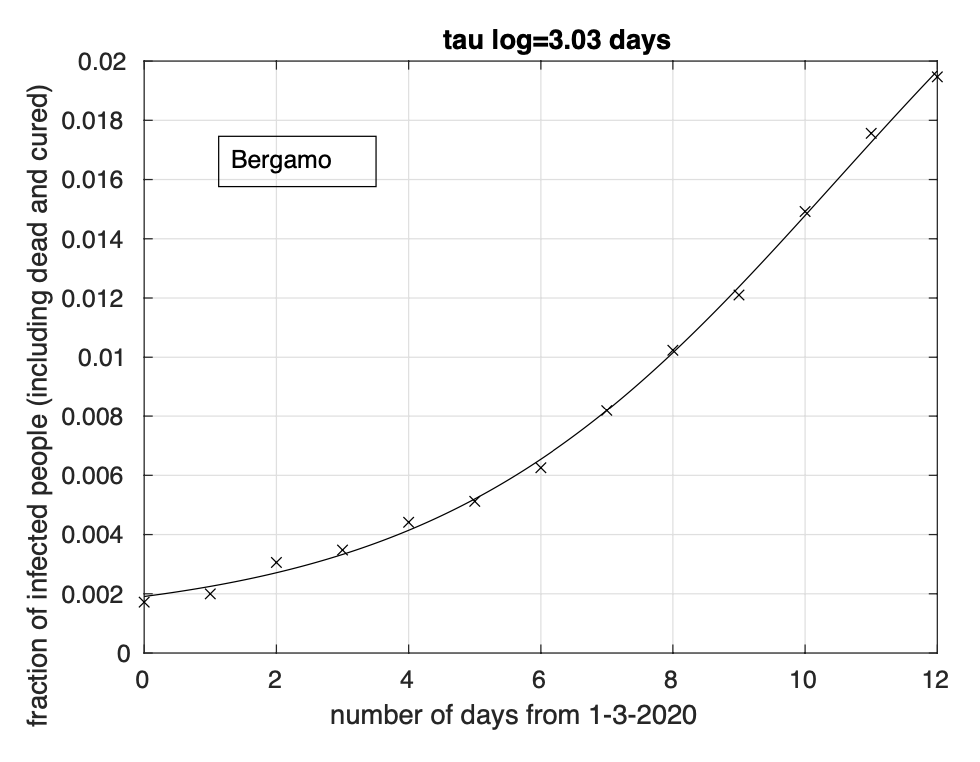
Figure 7: Sequenza della frazione dei contagiati osservati nella provincia di Bergamo rispetto alla popolazione della provincia. Il miglior fit con un modello logistico è sovrapposto ai dati.
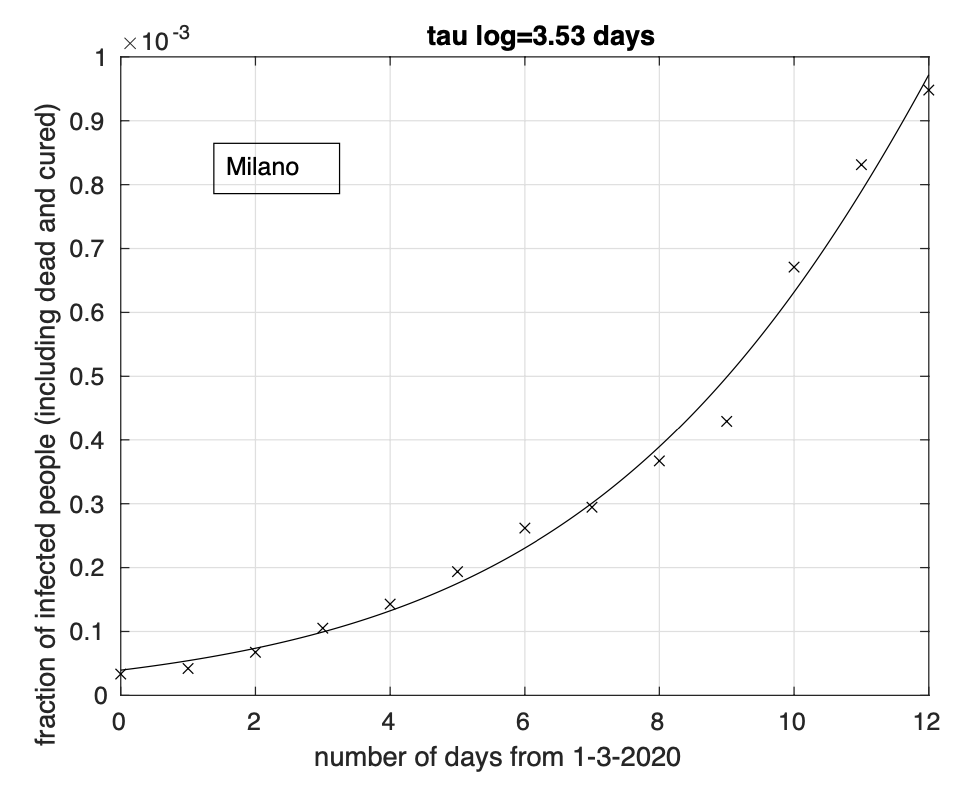
Figure 8: Sequenza della frazione dei contagiati osservati nella provincia di Milano rispetto alla popolazione della provincia. Il miglior fit con un modello logistico è sovrapposto ai dati.
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche
