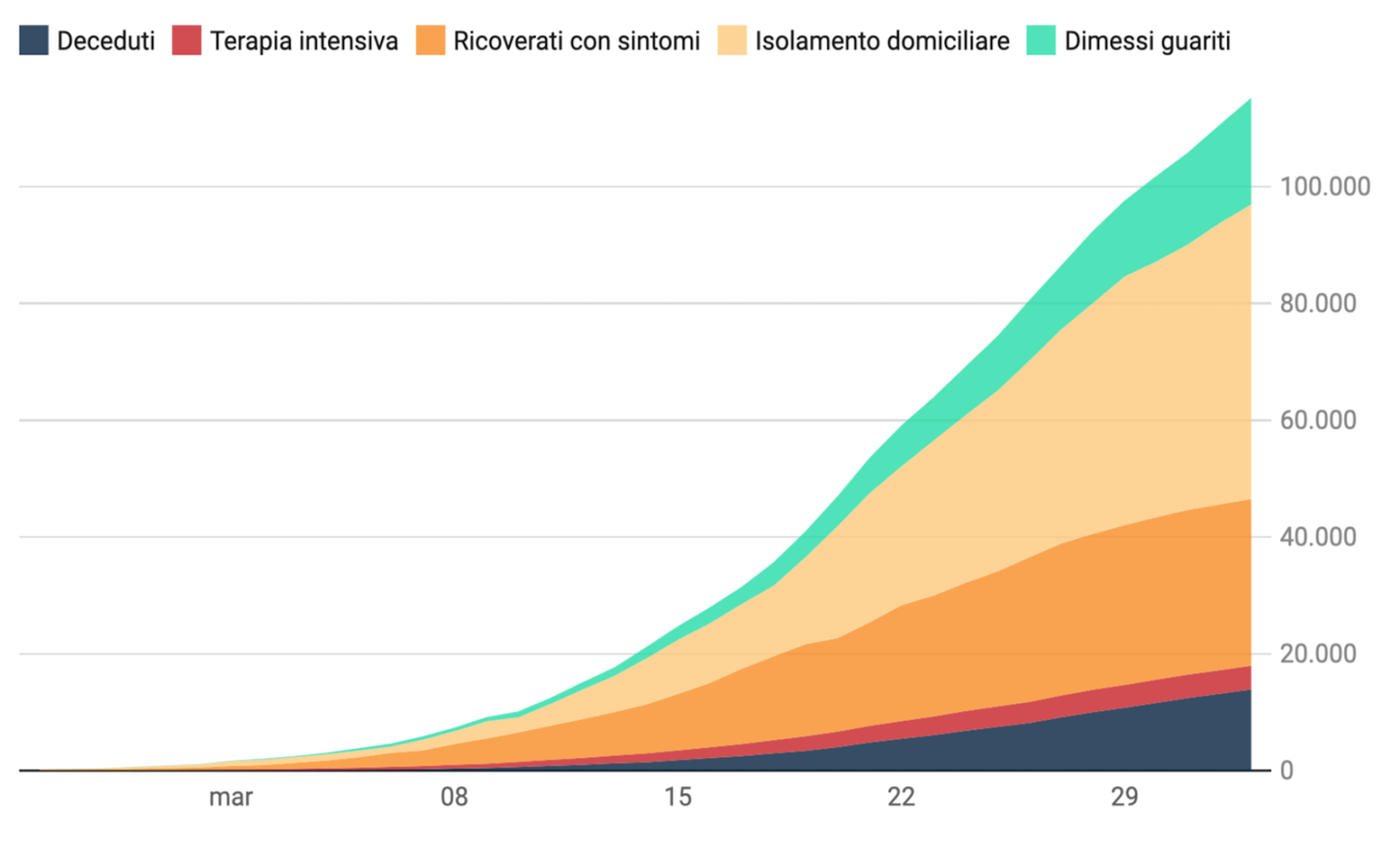
L’analisi delle sequenze temporali della frazione dei contagiati osservati rispetto alla popolazione della provincia rivela che 96 delle 107 province presentano una diminuzione del tasso di crescita. Mancano all’appello le province di Asti, Firenze, Massa e Carrara, L’Aquila, Rieti, Napoli, Campobasso, Taranto, Agrigento, Oristano e Sassari. Come si può vedere, le province ancora mancanti sono situate quasi esclusivamente al sud e nelle isole (i risultati di tutte le province analizzate possono essere scaricati qui). Questo è facilmente interpretabile alla luce del fatto che questa epidemia ha avuto un’origine localizzata in Lombardia da dove si è poi diffusa alle regioni più vicine e successivamente a quelle più lontane del sud.
Assieme a Marco Massa dell’Imperial College di Londra continuiamo a effettuare giorno per giorno un’analisi a livello regionale per la previsione del tempo in cui si stabilizzerà il numero dei contagiati osservati o equivalentemente avremo valori trascurabili del tasso di crescita di tale numero. L’analisi avviene nell’ambito statistico bayesiano ed è basata su un modello a compartimenti specifico per questo tipo di fenomeno (vedi nota metodologica). L’analisi ha rivelato che nelle tre regioni più colpite, Lombardia, Emilia Romagna e Veneto, il tasso di crescita del numero osservato dei contagiati raggiungerà valori trascurabili durante le ultime due decadi di maggio (vedi figura 1).
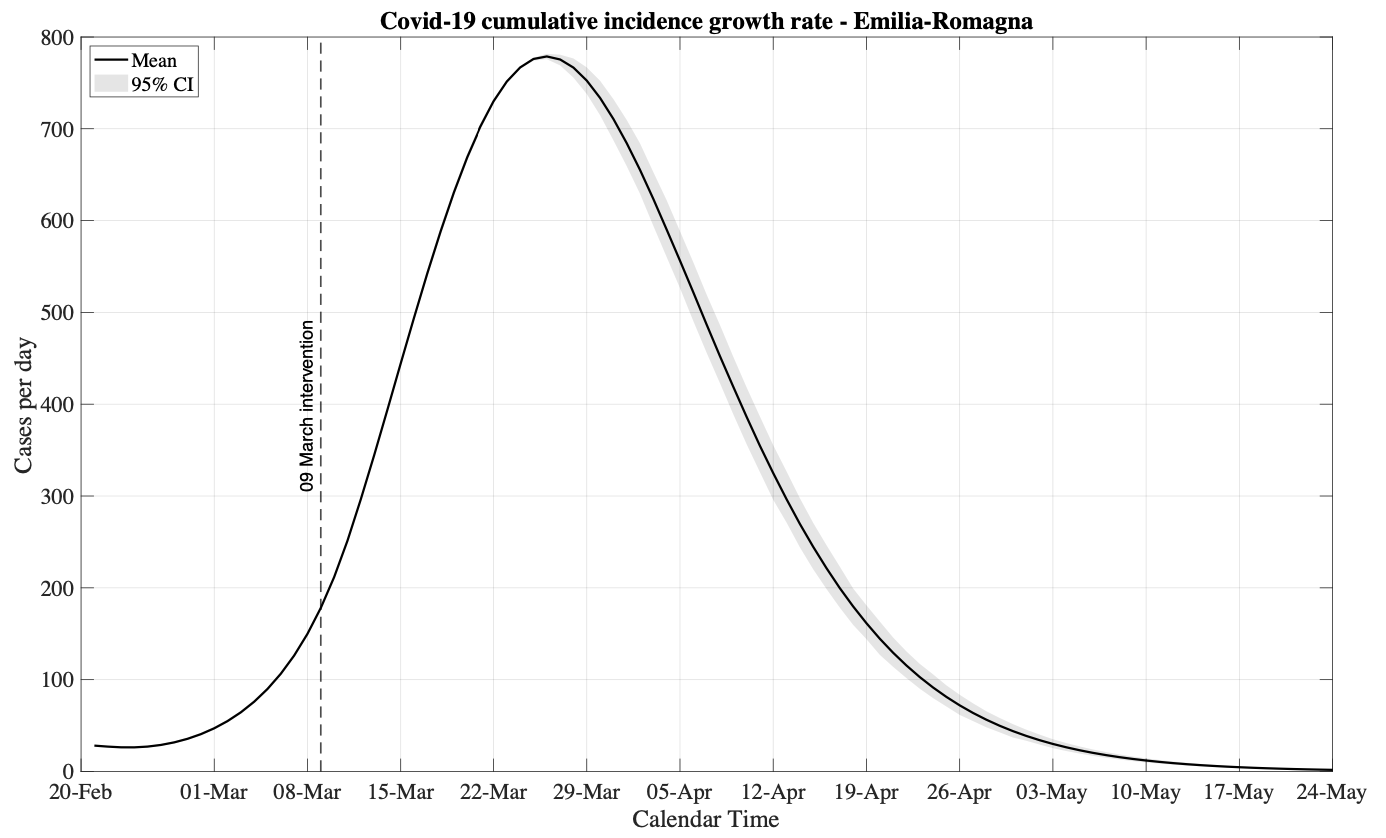
Figura 1. Previsione del tasso di crescita del numero di contagiati osservati in Emilia Romagna ottenuta con l’approccio statistico bayesiano basato sul modello a compartimenti.
E' molto importante sottolineare in primo luogo che questa stima può cambiare nel tempo e viene quindi aggiornata ogni giorno. Inoltre, il risultato vale se non cambierà l’ipotesi sul comportamento virtuoso degli italiani rispetto alle misure di riduzione del rischio di contagio introdotte dal governo. E quindi fondamentale che ciascuno di noi continui a fornire il proprio contributo, da solo trascurabile, ma che sommato a quelli di tutti gli altri, ha generato l’effetto osservato di frenata della diffusione dell’epidemia.
Ci occupiamo ora di alcuni aspetti che caratterizzano i pesanti effetti dell’epidemia di coronavirus sulla salute pubblica in termini di vite umane perse. Oggi ci concentriamo sull’andamento temporale dell’indice di mortalità, definito come il rapporto tra il numero di decessi e il numero di abitanti nella zona considerata. L’analisi è stata condotta a livello regionale, che è quello più fine per il quale abbiamo a disposizione i dati sui decessi. Rimandiamo al documento del 19 Marzo per alcune considerazioni sui problemi e sugli errori che influenzano il valore misurato del numero di decessi.
Abbiamo studiato quattro regioni, la Lombardia, origine della diffusione dell’epidemia in Italia e le tre regioni con essa confinanti dove si sono registrati i maggiori danni in termini sanitari: Emilia Romagna, Piemonte e Veneto.
In figura 2 mostriamo l’evoluzione nel tempo del numero di morti per coronavirus per 100,000 abitanti per le quattro regioni considerate.
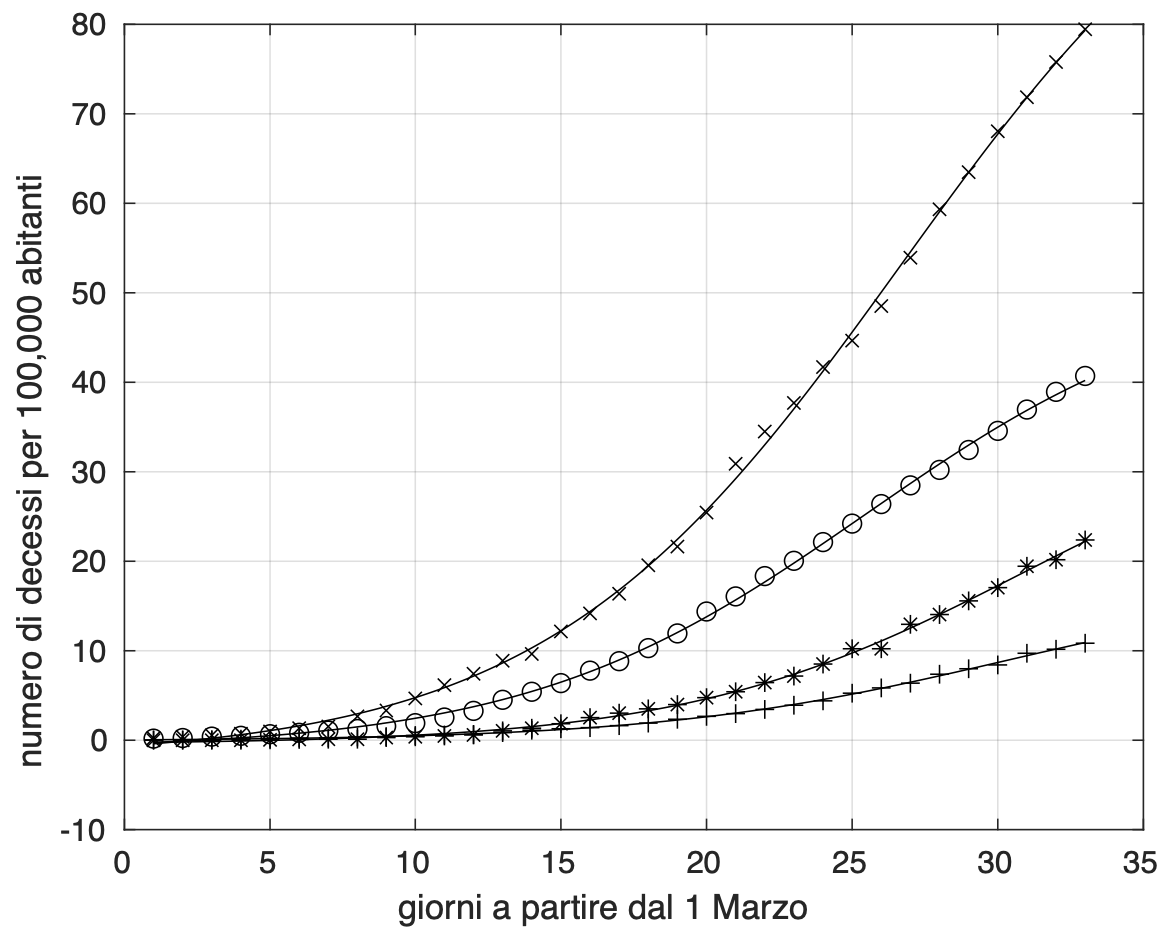
Figura 2. Andamento temporale del tasso di mortalità per coronavirus per la Lombardia (x), l’Emilia Romagna (o), il Piemonte (*) ed il Veneto (+).
I dati misurati sono stati descritti da un modello logistico (vedi nota metodologica), sovrapposto ad essi nella figura. E' da notare il comportamento virtuoso del Veneto, dove riscontriamo la curva più bassa del tasso di mortalità. Una spiegazione di ciò potrebbe essere legata al basso grado di ospedalizzazione dei pazienti nella regione Veneto, 30% circa, da confrontare per esempio con quello della Lombardia, pari circa al 60%. E' infatti noto che una via di diffusione molto efficace di questa malattia è quella nosocomiale.
A livello visivo si nota un andamento simile delle quattro curve. Questo ha suggerito di calcolare il coefficiente di determinazione per quantificare la similarità tra le curve (vedi tabella 1).
| Lombardia | Emilia Romagna | Piemonte | Veneto | |
|---|---|---|---|---|
| Lombardia | 1 | 0,9986 | 0,9795 | 0,9859 |
| Emilia Romagna | 0,9986 | 1 | 0,9728 | 0,9802 |
| Piemonte | 0.9795 | 0,9728 | 1 | 0,9973 |
| Veneto | 0,9859 | 0,9802 | 0,9973 | 1 |
Tabella 1. Valori calcolati del coefficiente di determinazione tra coppie di curve di mortalità.
Esso è il quadrato del coefficiente di correlazione lineare tra le sequenze numeriche di una generica coppia di curve ed è compreso tra zero ed uno. Tanto più il valore è vicino a uno, quanto più le curve sono simili. Dai valori della tabella possiamo dire che per due delle sei coppie di curve, Lombardia - Emilia Romagna e Piemonte - Veneto, c’è una forte similarità tra le curve della coppia. Abbiamo qundi effettuato un fit lineare per ciascuna delle due coppie (vedi figure 3 e 4). E' sorprendente la vicinanza tra i due valori stimati della costante moltiplicativa del modello lineare: 0,52 per Lombardia - Emilia Romagna e 0,49 per Piemonte - Veneto.
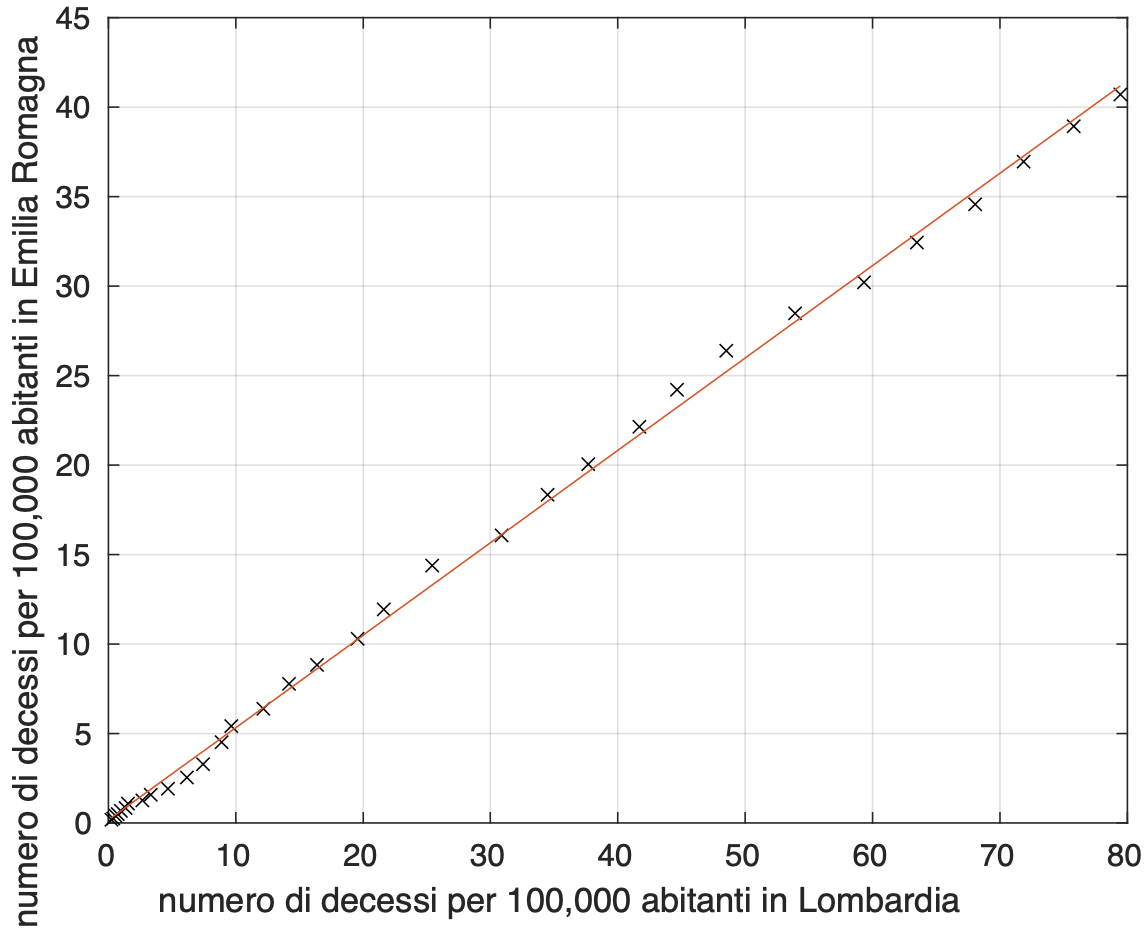
Figura 3. Dipendenza lineare tra i valori del tasso di mortalità nel tempo in Lombardia e quelli in Emilia Romagna.
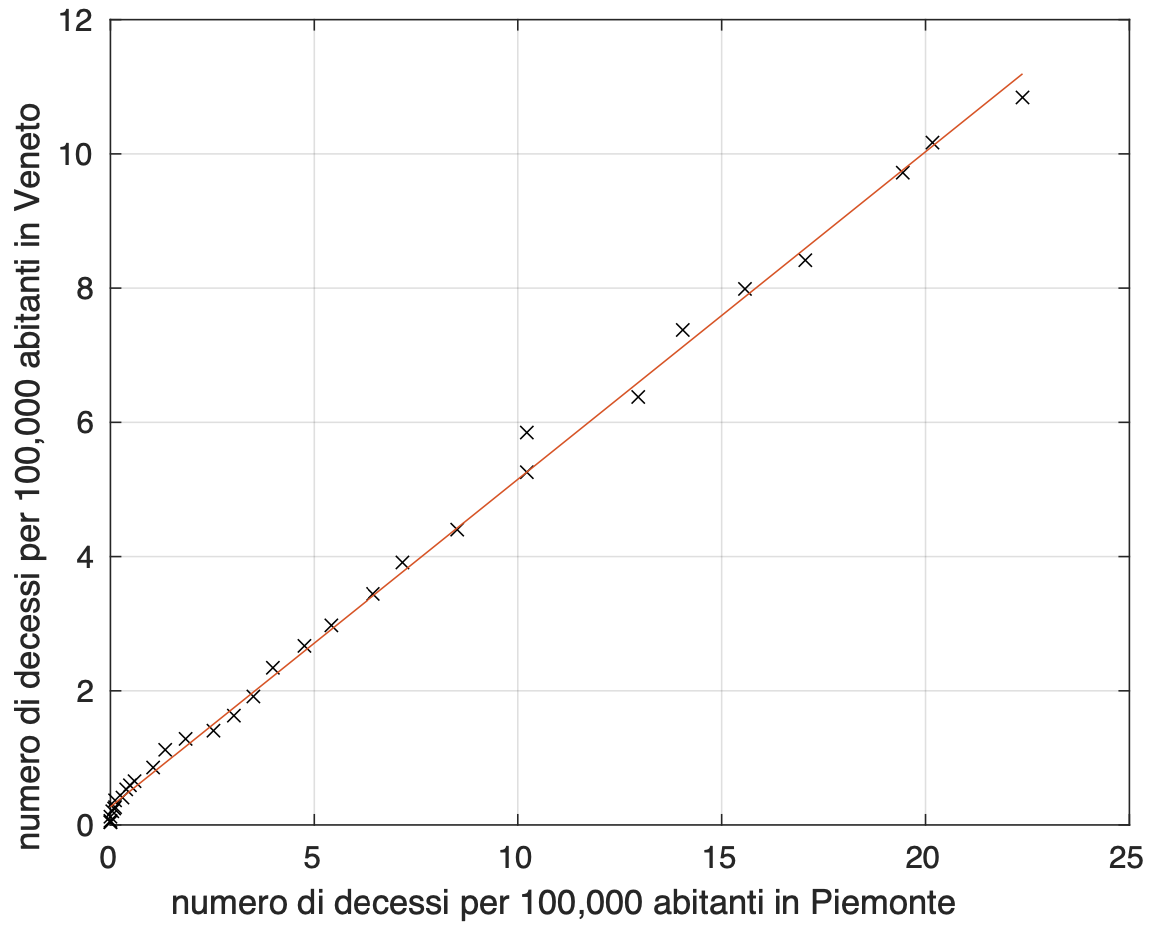
Figura 4. Dipendenza lineare tra i valori del tasso di mortalità nel tempo in Piemonte e quelli in Veneto.
Nota
In questo documento sono descritti i risultati relativi all’analisi per tutte le province di ciascuna regione. I dati utilizzati sono quelli aggiornati alle 18 del 2 Aprile 2020 e sono stati scaricati dal sito https://github.com/pcm-dpc/COVID-19/tree/master/dati-province. I risultati sostituiscono o integrano quelli nel documento del 27 Marzo. Valgono le stesse considerazioni generali del documento del 27 Marzo. Alcuni chiarimenti possono essere trovati nella Nota Metodologica. I risultati di tutte le province possono essere scaricati qui.
Scarica questo documento in versione pdf.
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche
Marco Massa
Dottorando e Graduate Teaching Assistant presso il Dipartimento di Matematica dell'Imperial College London
