In questo documento sono descritti i risultati relativi all’analisi per tutte le province di ciascuna regione. I risultati sostituiscono o integrano quelli nel documento del 20 Marzo. I dati utilizzati sono quelli aggiornati alle 18 del 21 Marzo 2020 e sono stati scaricati dal sito https://github.com/pcm-dpc/COVID-19/tree/master/dati-province. Valgono le stesse considerazioni generali del documento del 20 marzo.
 Notiamo che per 31 delle 107 province la curva della frazione dei contagiati osservati mostra un iniziale aumento del tasso crescita fino a raggiunngere un massimo per poi diminuire.
Notiamo che per 31 delle 107 province la curva della frazione dei contagiati osservati mostra un iniziale aumento del tasso crescita fino a raggiunngere un massimo per poi diminuire.
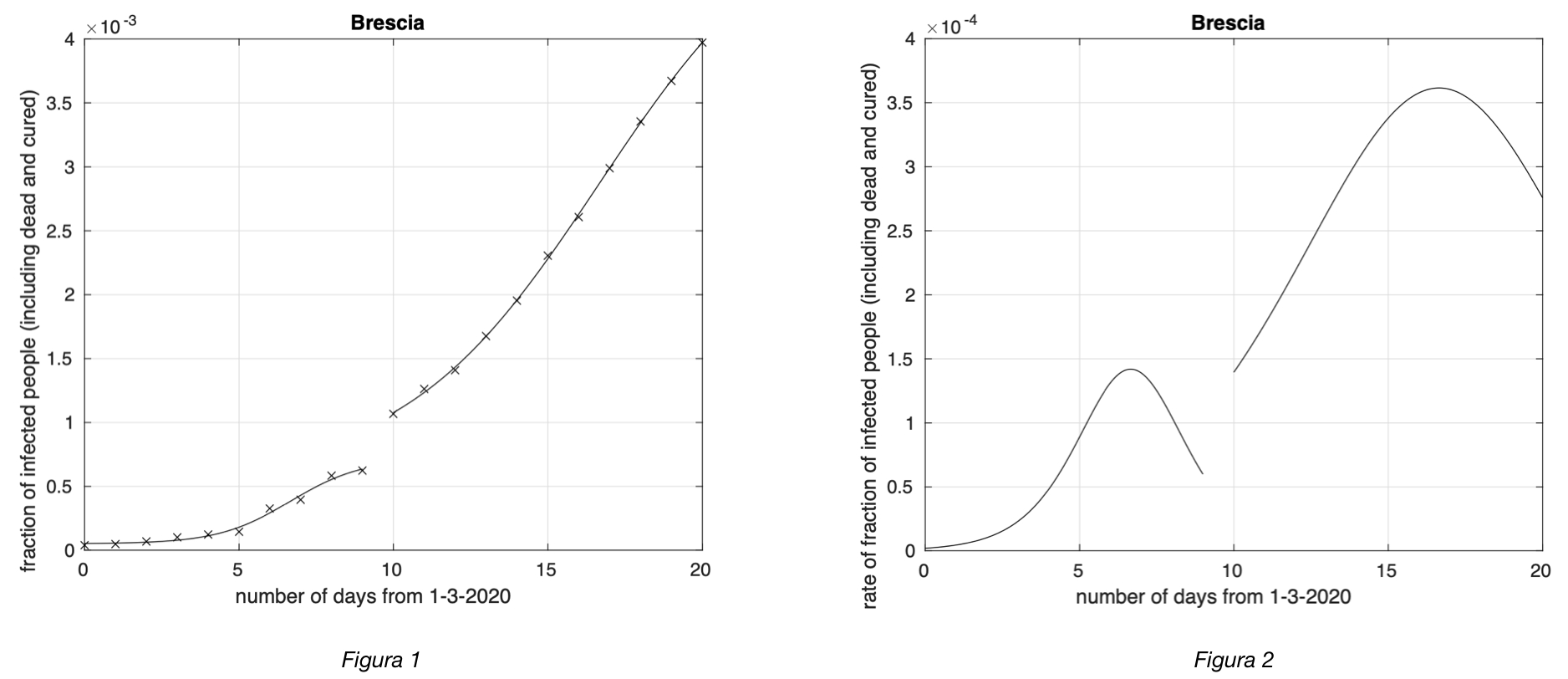
Improvvisamente verso l’11-12 marzo si ha successivamente un’inversione di tendenza e il tasso torna di nuovo a salire (vedi per esempio figure 1 e 2). Ipotizziamo che questo sia stato causato dall’impulso alla diffusione dell’epidemia dato dai fenomeni collettivi degli assalti ai treni e degli assalti ai supermercati avvenuti il 7-8 marzo in relazione al decreto che istituiva la zona rossa in Lombardia.
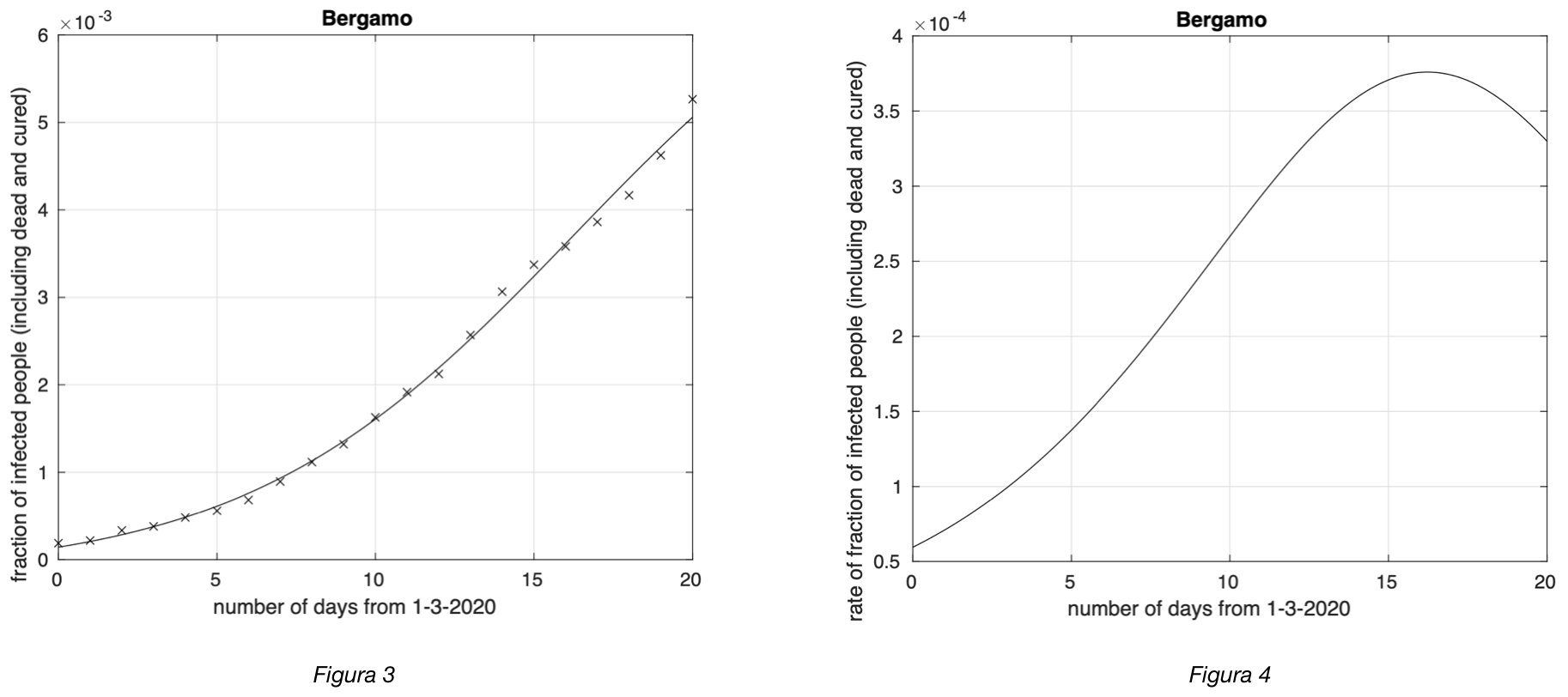 Per 64 delle 107 province i grafici mostrano evidenza di riduzione del tasso nella seconda parte dell’intervallo temporale (vedi per esempio figure 3 e 4). Ipotizziamo che questo sia stato causato dalla riduzione della diffusione indotta dalle misure di limitazione della mobilità introdotte col decreto “Io resto a casa” dell’11 marzo. Per le tre regioni maggiormente colpite, Lombardia, Emilia e Veneto, le province che mostrano questa diminuzione del tasso di crescita sono Bergamo, Brescia, Como, Cremona, Lodi, Monza, Pavia, Sondrio, Varese per la Lombardia, Piacenza, Parma, Reggio Emilia. Bologna, e Forlì Cesena per l’Emilia e Verona, Vicenza, Padova, Treviso per il Veneto. Per vedere i grafici di tutte le province, cliccare qui.
Per 64 delle 107 province i grafici mostrano evidenza di riduzione del tasso nella seconda parte dell’intervallo temporale (vedi per esempio figure 3 e 4). Ipotizziamo che questo sia stato causato dalla riduzione della diffusione indotta dalle misure di limitazione della mobilità introdotte col decreto “Io resto a casa” dell’11 marzo. Per le tre regioni maggiormente colpite, Lombardia, Emilia e Veneto, le province che mostrano questa diminuzione del tasso di crescita sono Bergamo, Brescia, Como, Cremona, Lodi, Monza, Pavia, Sondrio, Varese per la Lombardia, Piacenza, Parma, Reggio Emilia. Bologna, e Forlì Cesena per l’Emilia e Verona, Vicenza, Padova, Treviso per il Veneto. Per vedere i grafici di tutte le province, cliccare qui.
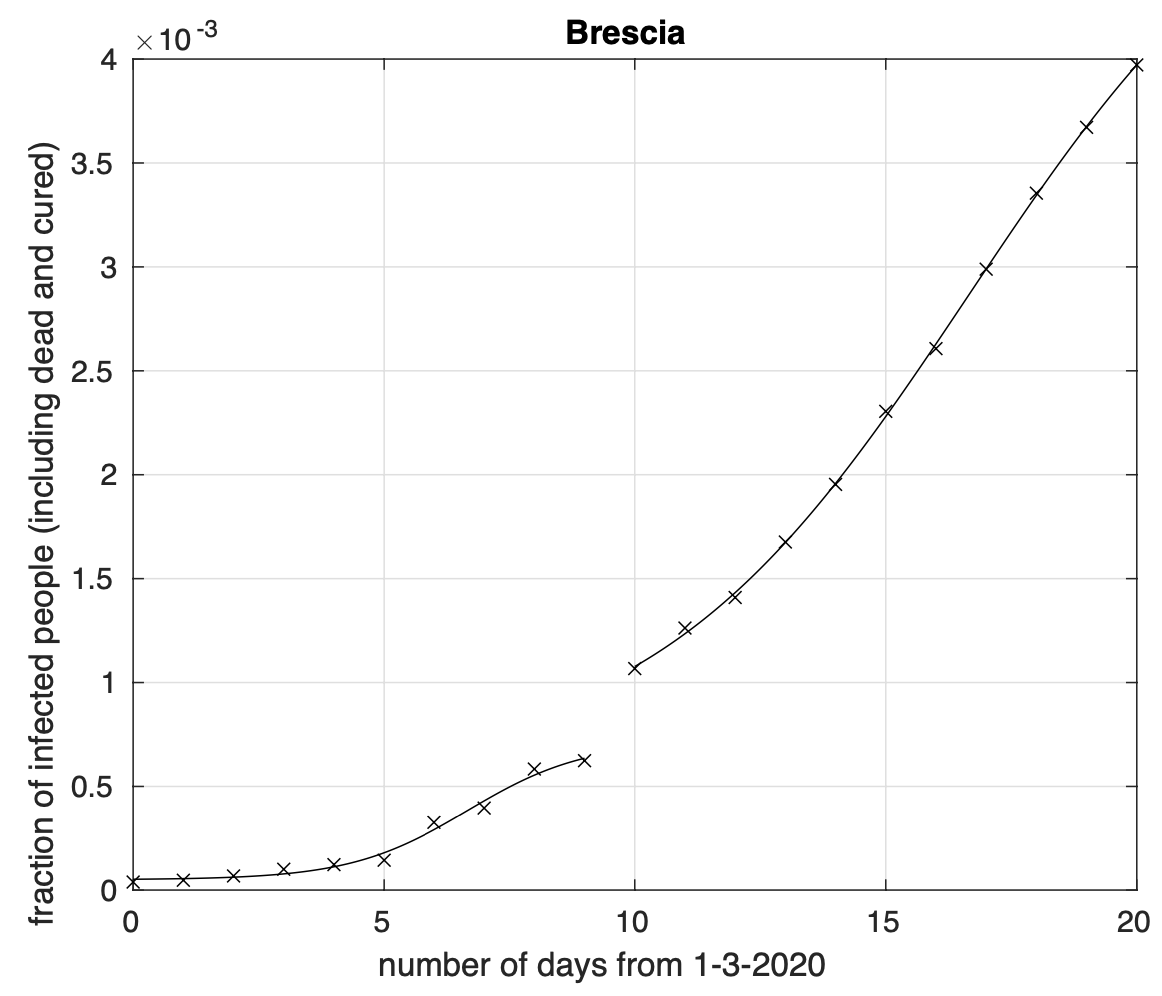
Figura 1. Frazione del numero di contagiati osservati nella provincia di Brescia rispetto alla popolazione della provincia in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello logistico è sovrapposto ai dati. Si osserva una fase in cui il tasso di crescita diminuisce. La curva della frazione dei contagiati, ossia coloro che sono al momento positivi al virus, o guariti o morti è per definizione crescente, o meglio "non decrescente". La rapidità con cui cresce la curva in un punto del tempo, il cosiddetto "tasso di crescita" si misura tramite la pendenza della retta tangente alla curva in quel punto. Più la pendenza è grande, più la curva cresce velocemente. Data una generica curva della frazione dei contagiati osservati al variare del tempo, possiamo costruire la curva che fornisce il tasso di crescita al variare del tempo. Quando il tasso inizia a diminuire la curva "flette", cioè cambia la sua concavità da verso l'alto a verso il basso e si appiattisce. Dopo un certo tempo, la curva non mostra più in pratica nessuna variazione.
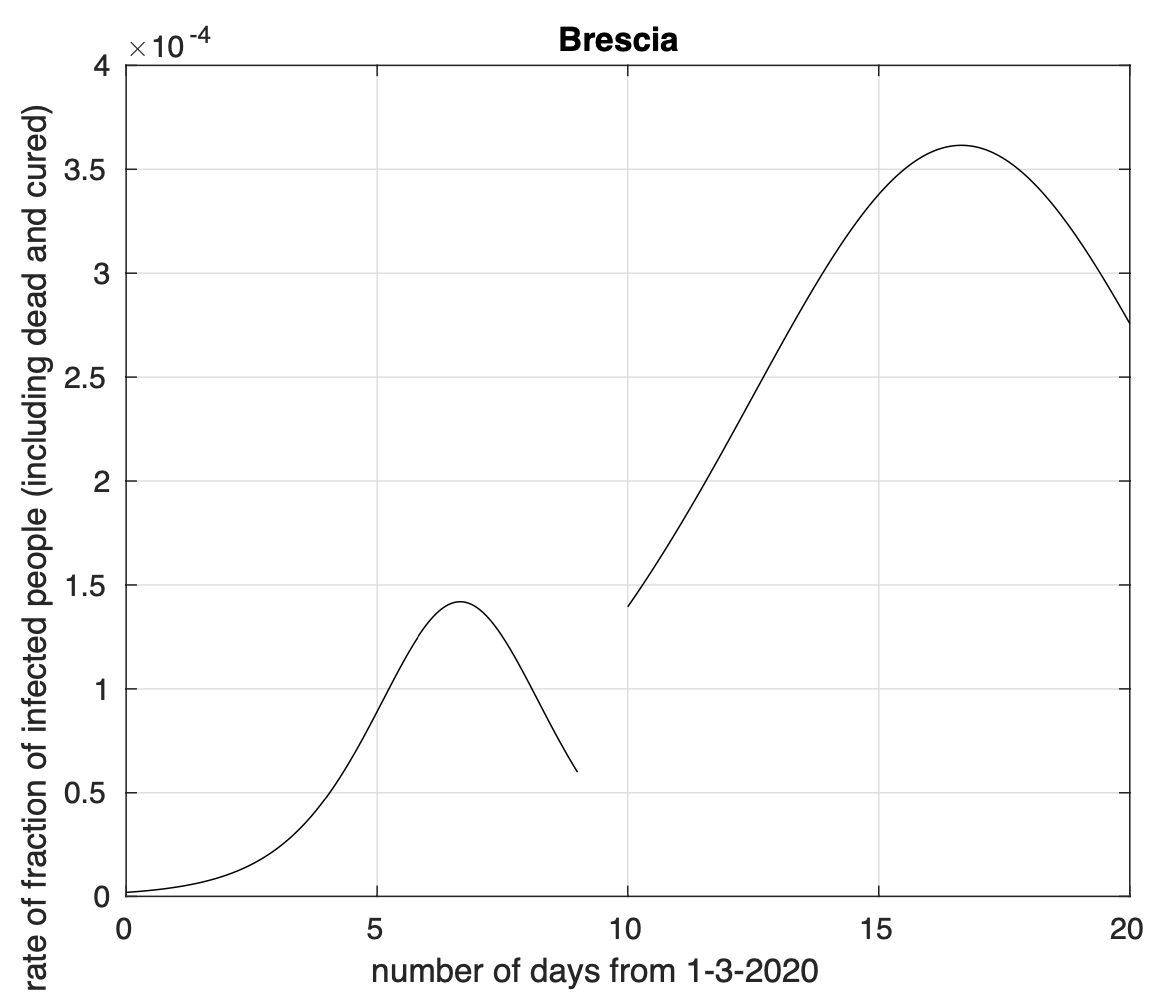
Figura 2. Tasso di crescita della frazione del numero di contagiati osservati a Brescia rispetto alla popolazione della provincia in funzione del tempo a partire dal 1 marzo. Il modello teorico adottato è quello logistico. Guardando la curva della frazione dei contagiati a Brescia, si vede che fino circa al 10 Marzo, l'andamento è quello "teorico" del fenomeno della diffusione dell'epidemia con la curva che diventa sempre più piatta. Poi, improvvisamente, attorno all'11 marzo si ha un'inversione di tendenza, la concavità torna di nuovo verso l'alto e il tasso torna a crescere.
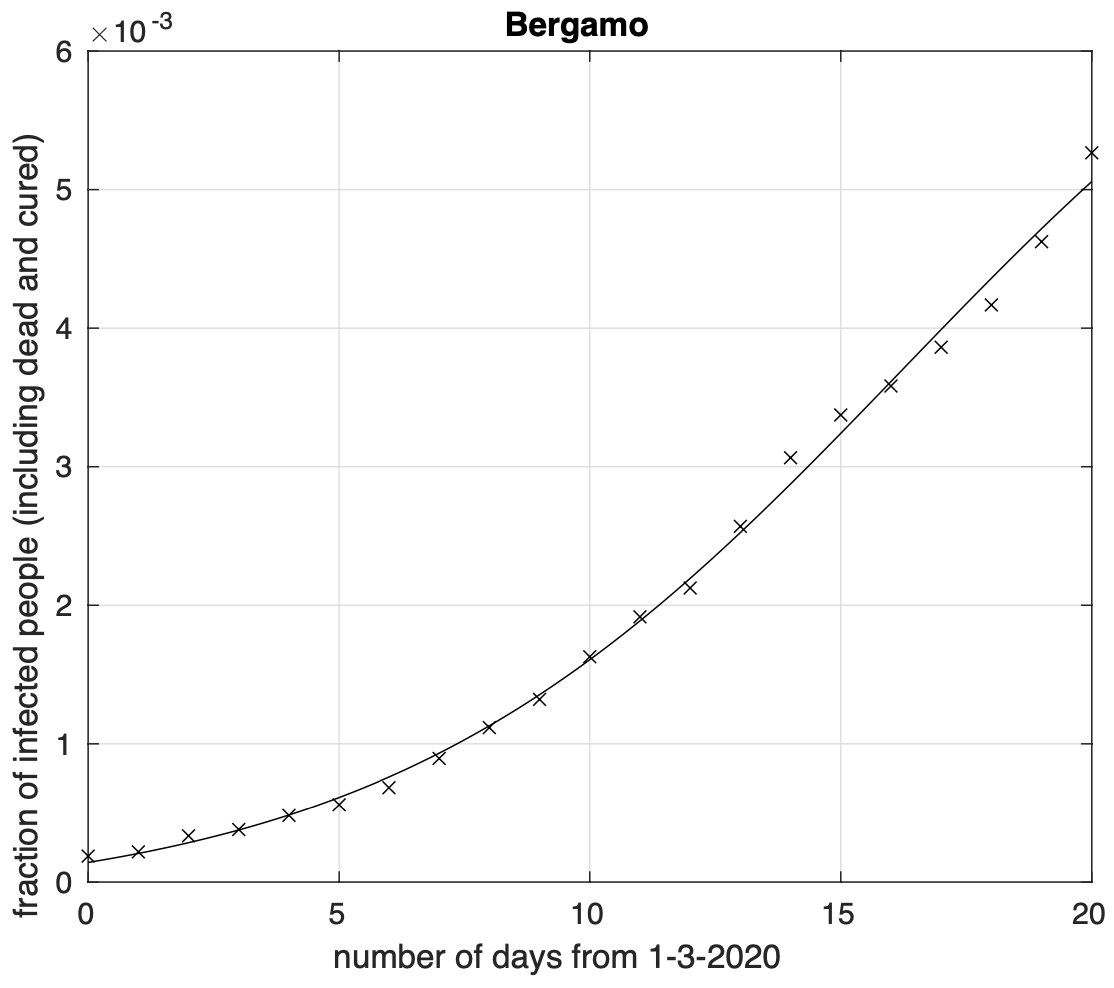
Figura 3. Frazione del numero di contagiati osservati nella provincia di Bergamo rispetto alla popolazione della provincia in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello logistico è sovrapposto ai dati. Si osserva una fase in cui il tasso di crescita diminuisce.
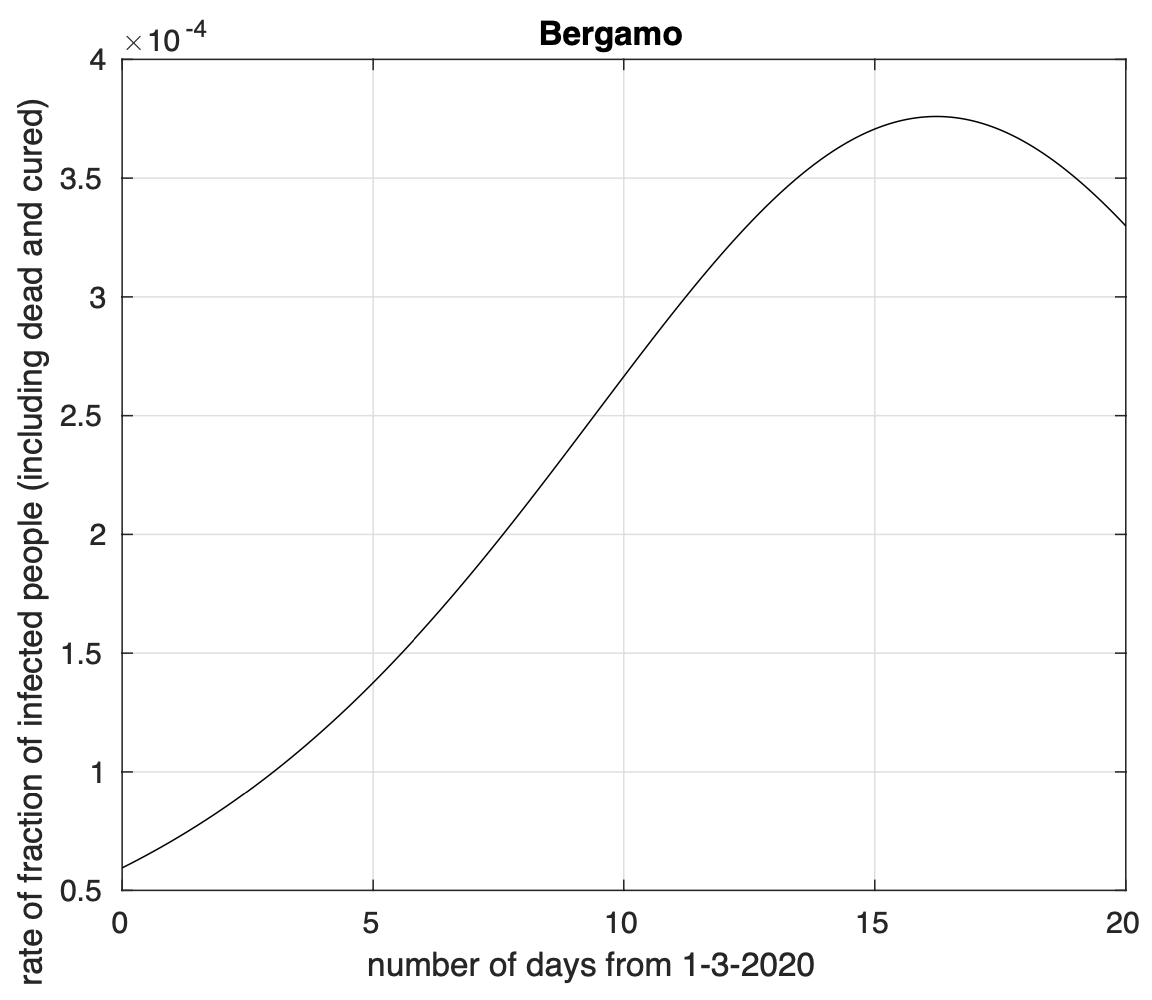
Figura 4. Tasso di crescita della frazione del numero di contagiati osservati a Bergamo rispetto alla popolazione della provincia in funzione del tempo a partire dal 1 marzo. Il modello teorico adottato è quello logistico.
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche

