
Wilensky, U. (1998). NetLogo Virus model. http://ccl.northwestern.edu/netlogo/models/Virus. Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL.
Recenti eventi hanno messo in evidenza la fragilità del sistema Terra, ma anche la consapevolezza di quanto la scienza e la ricerca scientifica possano fornire contributi importanti a interventi a volte tanto urgenti, quanto indispensabili. Questa crescita culturale è stata indotta sia dal sempre più visibile degrado del pianeta, con cambiamenti climatici che hanno generato veri e propri disastri ambientali, sia dalla pandemia causata dal virus SARS-CoV-2. La pandemia ha cambiato la nostra vita, l’organizzazione sociale e l’economia nel suo complesso. È necessario correre ai ripari.
La considerazione del premio Nobel Giorgio Parisi è centrale: il pianeta Terra sopravviverà, a rischio sono gli uomini. Quindi è necessario non solo riparare, ma anche prevenire [1].
I modelli matematici possono contribuire a progettare questi interventi, nel quadro del complesso dialogo fra scienze naturali e società. Infatti, le scienze matematiche sono in grado di interpretare, con metodi rigorosi, i risultati scientifici che le scienze naturali, ad esempio biologia e medicina, ci forniscono. Questa affermazione, apparentemente solo costruttiva, va comunque ulteriormente rivista evidenziando non solo gli aspetti positivi dei modelli, ma anche i loro limiti. In sintesi, occorre sia limitare le aspettative, a volte eccessive, sul ruolo delle scienze definite “esatte”, e sia comprendere il percorso che i matematici dovrebbero necessariamente seguire nella derivazione dei loro modelli. Inoltre, è necessario che i matematici comprendano che l’invenzione di nuove teorie è un passaggio obbligato per interpretare, e quindi descrivere, le dinamiche dei sistemi viventi. In altri termini, la matematica della materia inerte non è adeguata a trattare la materia vivente, come ben risulta dall’analisi critica del premio Nobel Lee Hartwell [2].
Il tema di una matematica dei sistemi viventi è trattato nel libro A Quest Towards a Mathematical Theory of Living Systems [3] ed è anche ripreso nell’articolo di Scienza in rete Il complesso dialogo fra matematica e pandemie. Tuttavia, prima di descrivere i contributi che la matematica può dare allo studio della pandemia è opportuno prendere coscienza della notevole complessità del sistema in esame. Non solo abbiamo l’interazione tra medicina e biologia, ma anche l’intera collettività è coinvolta con i suoi problemi sociali ed economici.
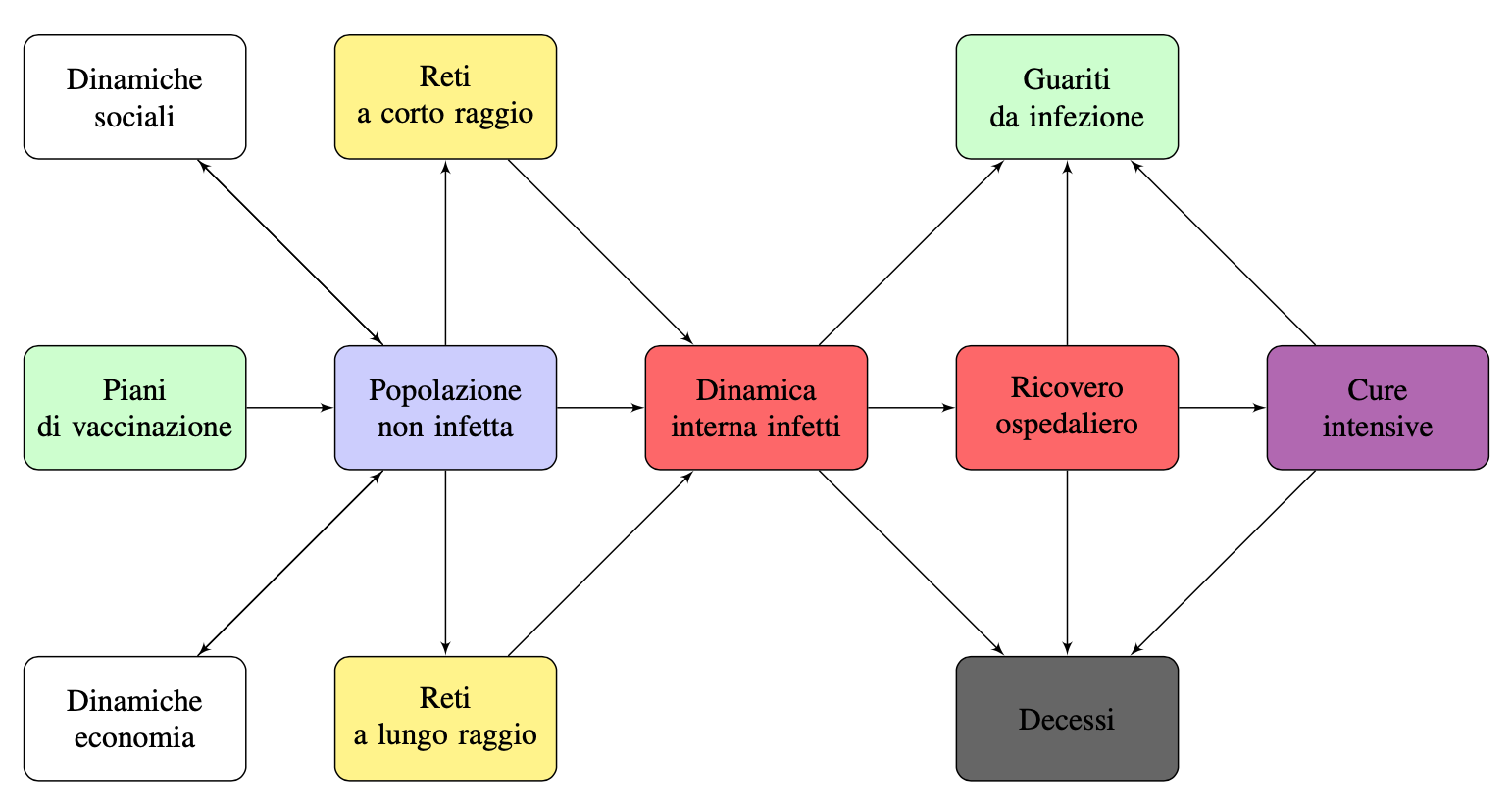
Figura 1. Una rappresentazione delle molte componenti, anche se non tutte, della complessa interazione che è indispensabile esaminare.
La figura 1 visualizza molte componenti, anche se non tutte, di questa complessa interazione. Lo studio matematico deve considerare ogni componente del flow-chart, evitando le semplificazioni che conducono a formule semplici, anzi semplicistiche, di facile comprensione, ma di scarsa utilità.
La ricerca scientifica si è attivata per fronteggiare una situazione di crisi che ha interessato tutte le nazioni con risultati utili anche se non ancora risolutivi. Si è anche cercato di coordinare azioni preventive e curative a livello di nazioni. Infatti, i numeri in gioco, l’impatto sulle strutture sanitarie e sui sistemi di produzione sono tali da richiedere un impegno particolarmente intenso. Indichiamo le ipotesi che hanno condotto ai modelli proposti in [4, 5].
- La derivazione del modello richiede un approccio a più scale: quella macroscopica corrisponde agli individui che possono essere infettati da dinamiche che coinvolgono anche la scala microscopica delle particelle del virus. Successivamente, la dinamica all’interno del soggetto infettato si sviluppa alla scala microscopica coinvolgendo particelle del virus e gli agenti del sistema immunitario. La scala molecolare (subcellulare) contribuisce alla comprensione delle dinamiche riproduzione del virus e quindi della reazione del sistema immunitario.
- L’entità del contagio non è una quantità generica, ma dipende dal livello di avanzamento dell’infezione del soggetto portatore, quindi da quella che viene definita carica virale. Inoltre, è una conseguenza anche di quella che viene definita distanza sociale fra individui. Per distanziamento, si intende l’insieme di azioni, generalmente indotte da normative, che riducono, o proteggono, il contatto fisico fra persone (mascherine, etc.).
- La competizione fra il virus proliferativo e il sistema immunitario inizia nei primi condotti del sistema respiratorio e successivamente prosegue negli organi infettati, prevalentemente nei polmoni. La dinamica include progressione (regressione) del livello di infezione.
- Il virus, nella fase di proliferazione, può mutare generando varianti che, se meno adatte all’ambiente, vengono soppresse dal sistema immunitario, o si affermano se più idonee. Si tratta di una dinamica post-darwiniana con probabilità di mutazione che cresce al crescere del livello globale di infezione nella popolazione.
- Programmi di vaccinazione possono essere sviluppati per incrementare la capacità di difesa del sistema immunitario. I vaccinati possono comunque infettarsi sebbene con livelli di carica virale decisamente inferiore a quella dei soggetti che non lo sono.
A partire dalle ipotesi 1–5 si deriva il modello matematico proposto in [4, 5]. Questo descrive la dinamica nel tempo delle densità numeriche dei seguenti soggetti: individui infettati sia dal virus originale e sia a causa delle varianti; ricoveri ospedalieri per crescenti livelli di terapia; decessi e guarigioni. Inoltre, il modello descrive come i processi di vaccinazione influenzano le dinamiche di infezione, ospedalizzazione, guarigione etc. Lo studio richiede un ben definito programma di vaccinazione, nel senso di numeri di vaccinati nel tempo anche in relazione al numero di soggetti coinvolgibili e delle relative tipologie di fragilità ovvero ruolo operativo (lavoro) nella società.
Alcuni esempi, fra i molti possibili, sono indicati nel seguito con rifermento alle dinamiche di due onde successive; la prima è controllata mediante azioni di distanziamento, mentre la seconda nasce per l’allentamento di quelle azioni. La coordinata verticale riporta le densità della popolazione infetta e la coordinata orizzontale il tempo. Questo è riferito all’intervallo di tempo che comprende la prima e la seconda onda. Le simulazioni effettuate sono molte e sono state via via aggiornate sulla base dei dati disponibili. Solo poche simulazioni, comunque esemplificative, sono riportate nel seguito. Tuttavia una sintesi globale dei risultati ottenuti è posta all’attenzione del lettore.
La figura 2 indica il risultato delle simulazioni sulla dinamica degli infetti per un virus con livello di aggressività fisso, considerando diversi livelli di distanziamento a seguito della riduzione del livello di distanziamento dopo la prima onda. In particolare una mancanza di controllo di tale livello può condurre a una seconda onda con numero di nuovi contagi superiore alla prima, come indicato nelle simulazioni con i colori blu, rosso e nero. Imponendo azioni di distanziamento più restrittive, la seconda onda presenta livelli di contagio inferiori a quelli della prima onda.
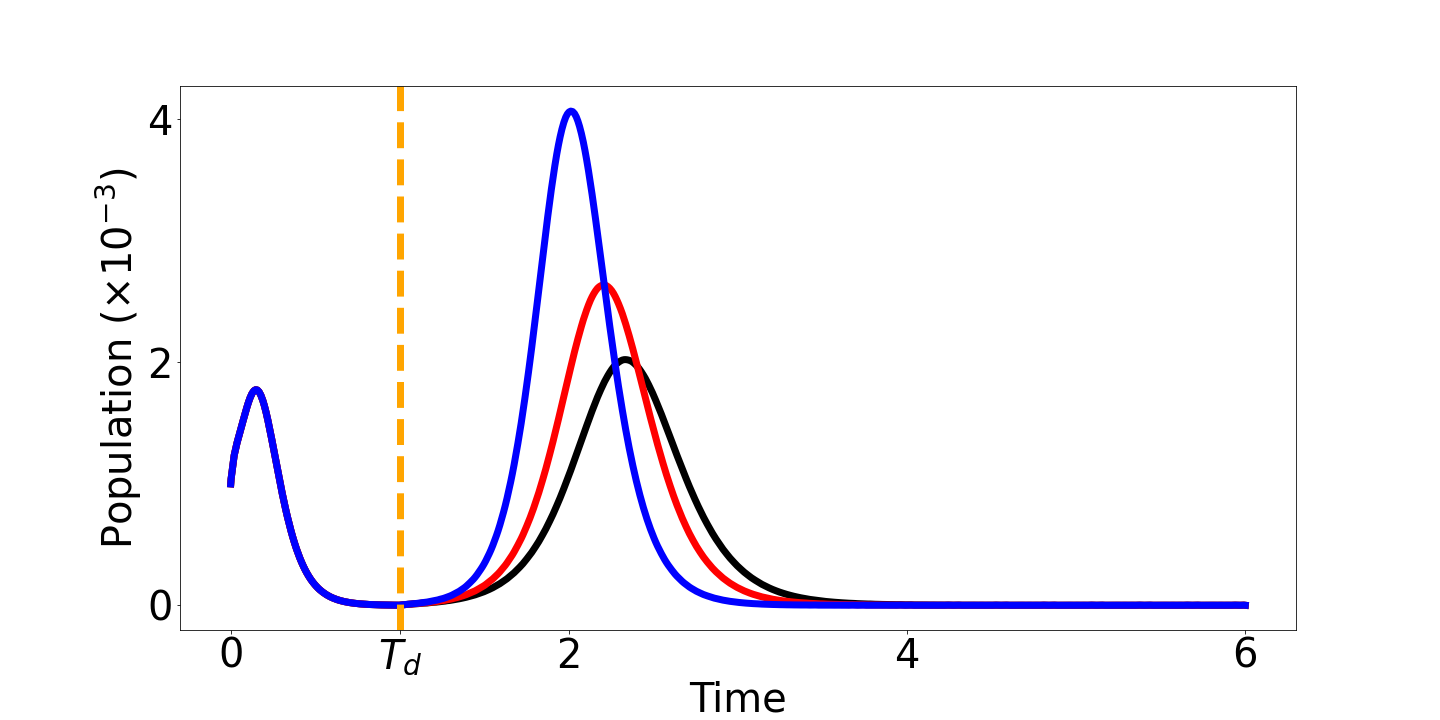
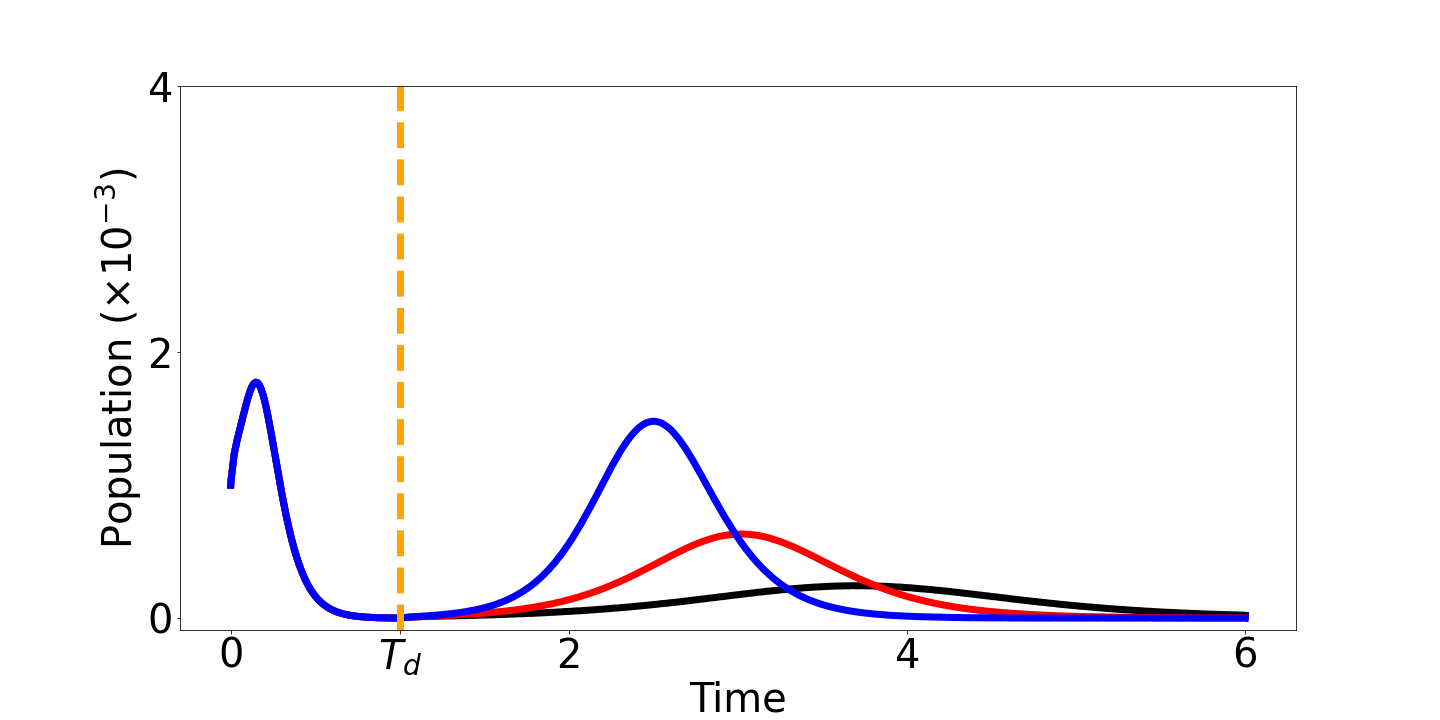
Figura 2. Densità di soggetti infetti nel tempo per diversi indici di distanziamento: nella figura in alto azioni di distanziamento elevati, nella figura in basso azioni ridotte.
La figura 3 visualizza come una variante maggiormente invasiva prevalga, quando la prima onda sembra aver esaurito la sua carica infettiva, rispetto al virus primario anche se nella prima onda la sua presenza risultava inferiore e apparentemente quando la prima onda sembra aver esaurito la sua carica infettiva.
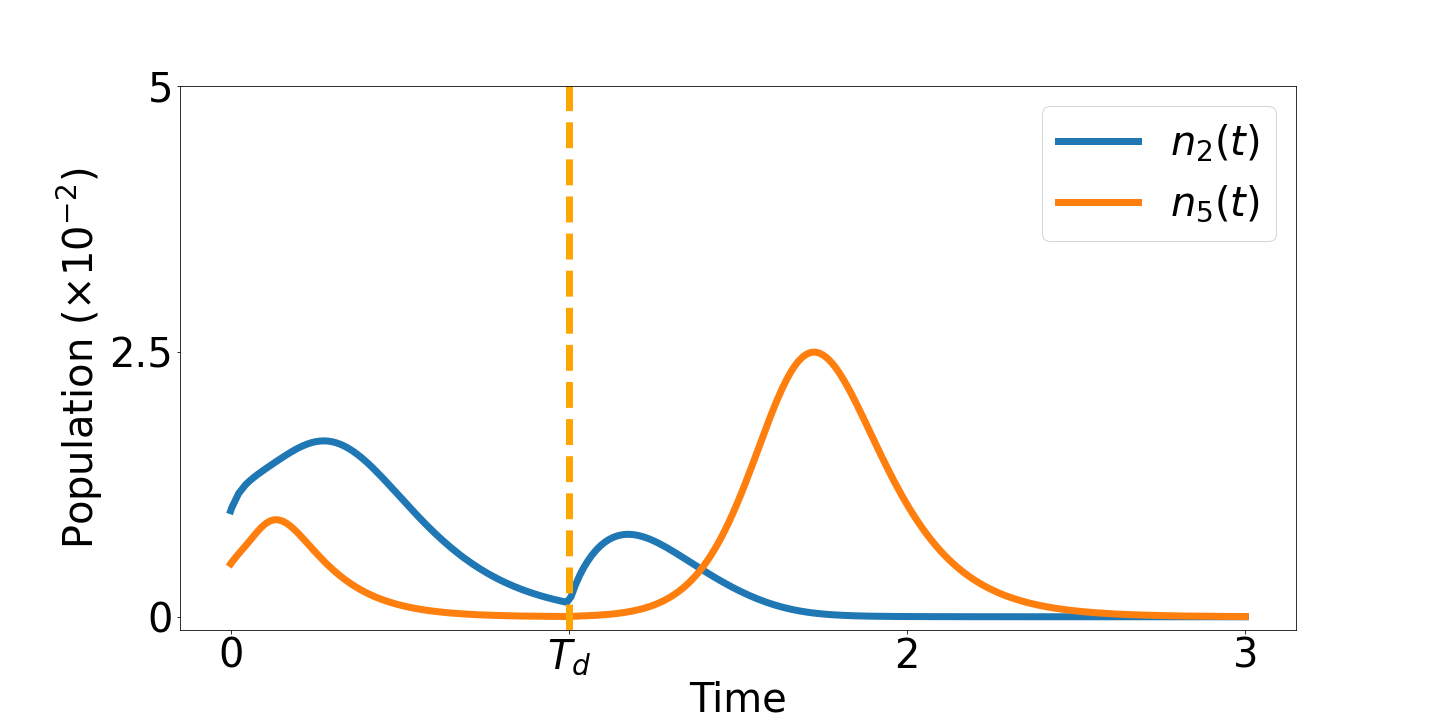
Figura 3. Densità di soggetti infetti nel tempo: da virus primario (blu) e da variante (arancione).
Infine, nella figura 4 osserviamo i possibili effetti di un programma di vaccinazione. La figura in alto corrisponde a una simulazione in assenza di processo di vaccinazione, mentre la figura in basso visualizza il ruolo di un processo di vaccinazione che riduce progressivamente il livello infettivo. Il modello prevede che anche i vaccinati possono essere soggetti a infezione. Tuttavia con livello patologico inferiore. Da segnalare che la figura 4 indica come un rilassamento precoce del distanziamento genera una seconda onda a elevato livello infettivo.
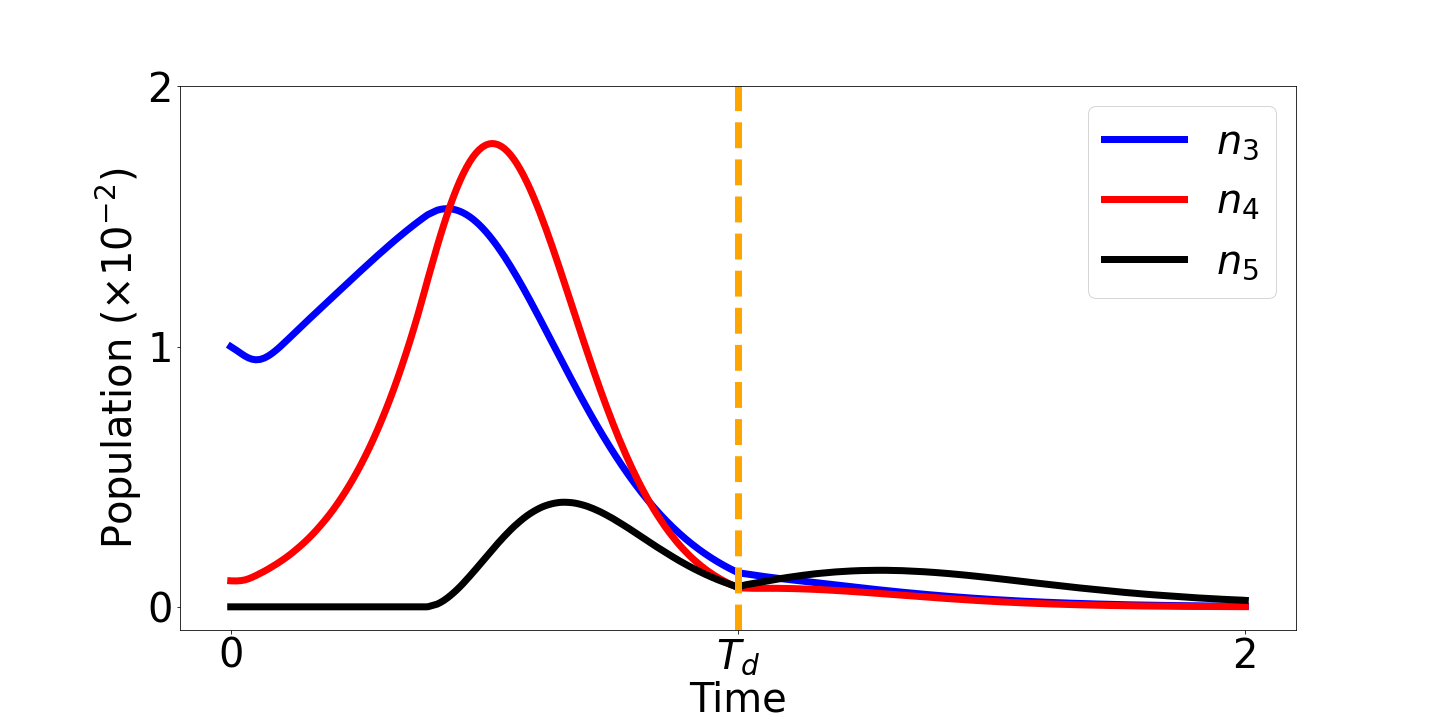
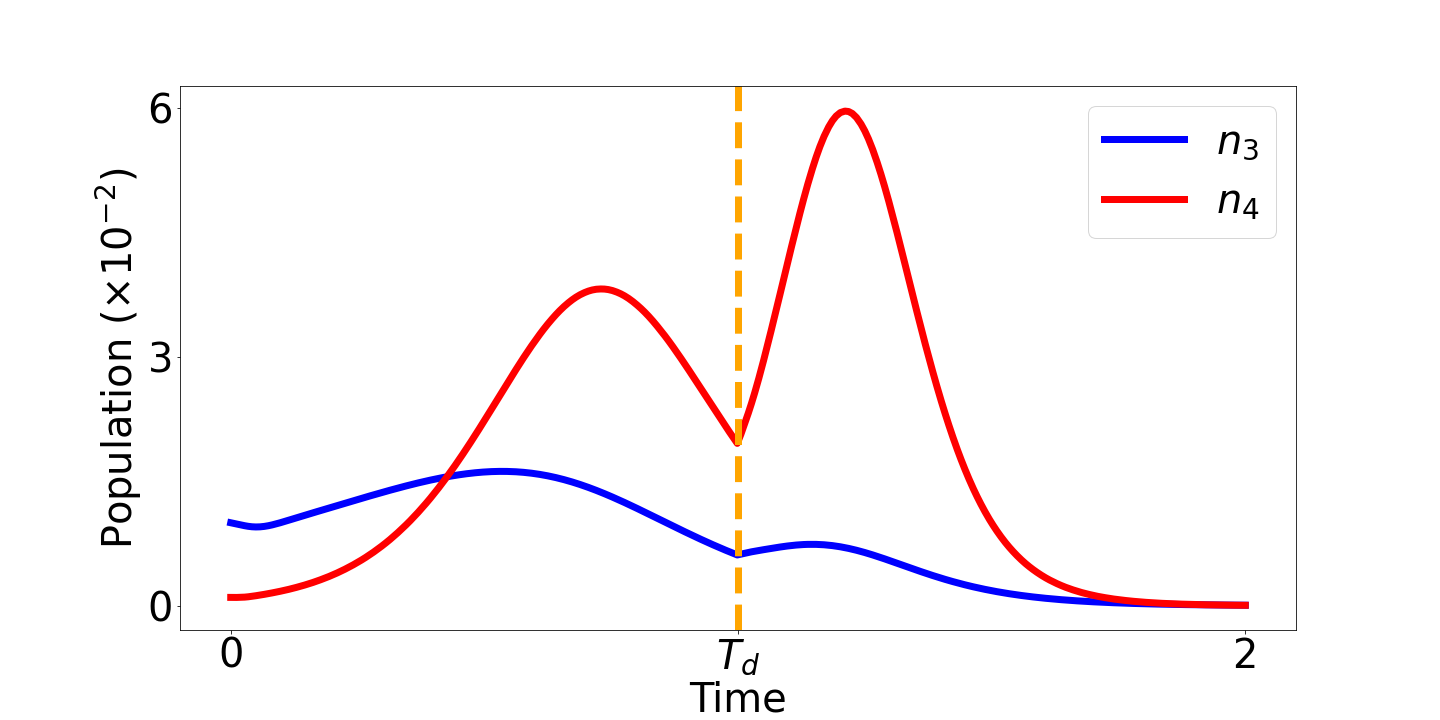
Figura 4. Densità di soggetti infetti nel tempo, da virus primario, variante e vaccinati.
Il complesso delle simulazioni prodotte conduce alle seguenti indicazioni:
- Anche dopo un elevato distanziamento, il virus continua a circolare e riprende vigore infettivo quando il distanziamento è allentato. La seconda onda risulta tanto più dannosa quanto maggiore è la riduzione.
- La variante è più aggressiva del virus primario e finisce con predominare, soprattutto nella seconda onda. La riduzione del distanziamento contribuisce al predominio della variante.
- Un piano di vaccinazione riduce di molto, soprattutto nella seconda onda, il numero degli infetti. Tuttavia, non annulla la circolazione del virus. Questo riprenderà nel momento in cui il distanziamento è rilassato.
- Un piano di vaccinazione non elimina il predominio della variante. Il modello indica come sia possibile anche il contagio dei vaccinati. Questi tuttavia richiedono livelli inferiori di terapia.
- Il modello matematico produce informazioni anche sui vari livelli della dinamica infettiva, in particolare, le infezioni che necessitano di ricoveri in cura intensiva ed anche il caso di decessi.
In sintesi, gli studi sviluppati in [3, 4] indicano come i modelli matematici siano in grado di svolgere un ruolo di supporto alla ricerca scientifica su problemi di interesse per la società. In merito a queste simulazioni va osservato quanto segue.
Le previsioni del modello sono state effettuate prima che il ruolo delle varianti fosse stato studiato a fondo e prima ancora che il processo di vaccinazione fosse attuato in modo significativo. Le simulazioni avevano già indicato che un processo di vaccinazione necessita, per migliorare la sua efficacia, di essere progettato in parallelo con un processo di parziale confinamento anche se impopolare. L'efficacia del primo, in assenza del secondo, si riduce notevolmente, anche se il risultato comunque positivo.
Pertanto, abbiamo visto come le previsioni fornite dal modello possano essere di supporto agli esperti che hanno il compito, anche politico, di sviluppare strategie intese a mitigare i danni in situazioni di crisi quali la pandemia in corso. Difficile trarre conclusioni, ci limitiamo quindi a individuare prospettive che meritano riflessioni ed interventi di chi governa la nazione.
Interazioni scientifiche: le ricerche di interesse per la società, come affermato in più punti, hanno carattere interdisciplinare. La pandemia in corso ha generato numerose ricerche interdisciplinari come documentato nell’articolo [4]. Le ricerche interdisciplinari, che hanno coinvolto le scienze matematiche, hanno contribuito al progresso in tutti i settori coinvolti, compresa la matematica stessa, ove lo stimolo da altri settori ha condotto a nuove teorie.
Politiche dei governi: i modelli matematici mettono a disposizione un insieme di scenari possibili di supporto al processo decisionale che deve tener conto del quadro completo che va dal reperimento delle risorse necessarie ai processi di crescita economica. Inoltre, i modelli contribuiscono non solo alle decisioni in situazioni di crisi conclamata, ma anche alla prevenzione di situazioni di crisi, in alcuni casi vere e proprie catastrofi. Ci sentiamo di aggiungere che il costo di prevenzione è, in molti casi, inferiore al costo di riparazione.
I progetti europei, di nostra esperienza diretta, hanno posto in evidenza come l'Unione europea promuova e supporti l’acquisizione di nuove competenze (skills). A livello europeo è in crescita l’attenzione a questo tipo di competenze. Nel sistema Italia, questo tipo di attenzione è decisamente inferiore a quello di altre nazioni. Il risultato è che le competenze formate in Italia prendono altre strade. Il riferimento è al rapporto OCDE: Getting skills right Italy (2017).
In conclusione, la ricerca scientifica in una visione interdisciplinare è una risorsa per l’umanità. Tuttavia, un cambio di mentalità appare necessario. Concludiamo quindi con le seguenti osservazioni:
- Il sistema delle imprese dovrebbe ulteriormente ampliare l’iniziativa imprenditoriale a sostegno dell’innovazione, in quanto motore di competizione a livello internazionale e quindi di sviluppo socio-economico del paese.
- L’accademia, a sua volta, dovrebbe sviluppare la capacità di rinnovarsi e introdurre processi meritocratici, riconoscendo anche la capacità di individuare tematiche di frontiera che aprano in dialogo fra scienze di base e problemi della società.
- Non sarà un arretramento culturale della ricerca di base in quanto dai problemi interdisciplinari nascono stimoli importanti allo sviluppo delle scienze di base, compresa la matematica.
Riferimenti bibliografici
1. P. Vineis, L. Carra, e R. Cingolani, Prevenire, Manifesto per una tecnopolitica, Giulio Einaudi, Editore, (2020).
2. Hartwell H.L., et all. From molecular to modular cell biology, Nature 1999; 402: c47-c52. https://doi.org/10.1038/35011540
3. N. Bellomo, A. Bellouquid, L. Gibelli, and N. Outada. A Quest Towards a Mathematical Theory of Living Systems. Birkha¨user-Springer, New York, 2017.
4. N. Bellomo, R. Bingham, M. Chaplain, G. Dosi, G. Forni, D. Knopoff, J. Lowengrub, R. Twarock, and M.E. Virgillito. A multi-scale model of virus pandemic: Heterogeneous interactive entities in a globally connected world. Mathematical Models and Methods in Applied Sciences 2020; 30: 1591-1651. https://doi.org/10.1142/S0218202520500323
5. N. Bellomo, D. Burini, and N. Outada. Pandemics of Mutating Virus and Society: A multi- scale active particles approach. Philosophical Transactions A, Royal Society, 2022, in stampa.


