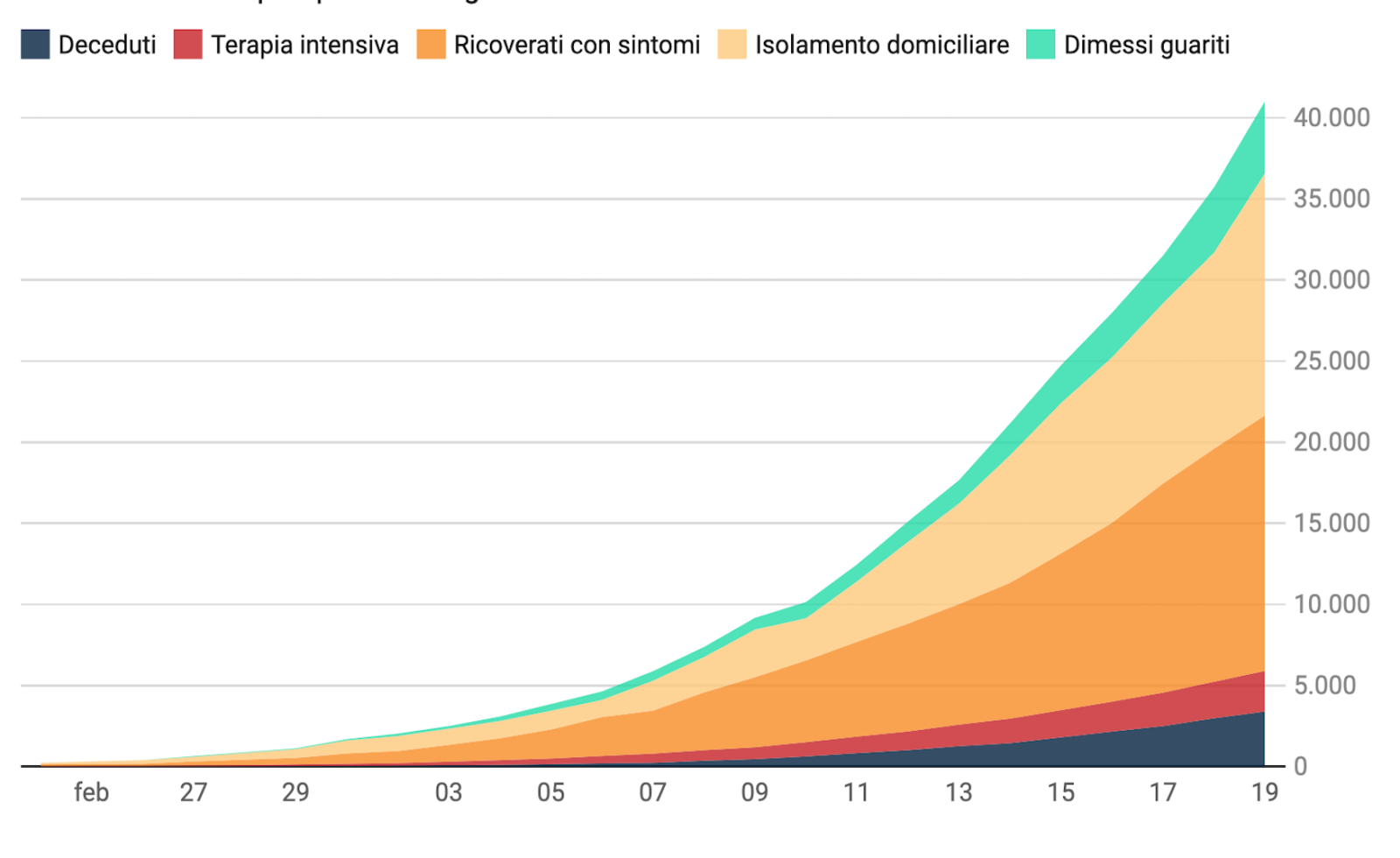
In questo documento sono descritti i risultati relativi all’analisi per le tre regioni maggiormente colpite, Lombardia, Emilia e Veneto, per le sei province della Lombardia al momento maggiormente colpite, per la provincia più colpita dell’Emilia e quella più colpita del Veneto. I dati utilizzati sono quelli aggiornati alle 18 del 19 marzo 2020, che sostituiscono o integrano quelli nel documento del 18 marzo. I dati a livello regionale sono stati scaricati dal sito https://github.com/pcm-dpc/COVID-19 e quelli a livello provinciale dal sito https://github.com/pcm-dpc/COVID-19/tree/master/dati-province.
Per quanto riguarda la Lombardia, si conferma anche per il 19 marzo la piccola ma progressiva riduzione del tasso di crescita della frazione dei contagiati osservati relativa ai giorni precedenti, come si può osservare nella figura 1 e in modo più evidente nella figura 2 che rappresenta, in funzione del tempo, proprio il tasso di crescita stimato a partire dai dati. Come detto in precedenza, ci aspettiamo che tale riduzione sia progressiva (se non intervengono altri fenomeni collettivi) e che sia dovuta all’introduzione delle misure restrittive sulla mobilità introdotte l’11 marzo. Rimandiamo ai prossimi sette giorni la verifica di questa ipotesi. Analoga situazione per il Veneto, come si può osservare nelle analoghe figure 3 e 4. Diverso è invece il comportamento dell’Emilia dove, con i dati disponibili fino ad oggi, non c’è evidenza di riduzione del tasso di crescita (vedi figure 5 e 6). Questo accade anche se adottiamo un modello più accurato di quello logistico come quello doppio logistico, come si osserva nelle figure 7 e 8.
A livello provinciale, per cinque delle sei province attualmente maggiormente colpite della Lombardia, Bergamo, Brescia, Cremona, Lodi, Milano, osserviamo una diminuzione del tasso di crescita, con delle differenze tra provincia e provincia, come mostrano le figure 9 e 10 per Bergamo e Brescia, rispettivamente. Per Milano (vedi figura 11) non c’è al momento evidenza di riduzione del tasso. In figura 12 possiamo vedere che per Lodi il tasso di crescita diminuisce costantemente sin da subito. Sarebbe quindi utile studiare nel dettaglio questo caso per capire da cosa dipenda questo comportamento peculiare indentificando eventualmente le principali cause, auspicando che siano legate ad alcune delle misure adottate per fronteggiare l’emergenza e al comportamento della popolazione.
Nella figura 13 vediamo il risultato per la provincia di Padova. Analogamente a quello che accade a livello regionale, anche per questa provincia si nota una riduzione del tasso di crescita. Come abbiamo visto dalle figure 5-8, per l’Emilia non osserviamo una riduzione del tasso. Dalla figura 14 possiamo invece vedere che la provincia di Piacenza mostra una riduzione del tasso di crescita, probabilmente determinata, come per gli altri casi, dall’introduzione delle misure di restrizione della mobilità col decreto “Io resto a casa” dell’11 marzo. Questo fatto suggerisce di effettuare le analisi su scale territoriali piccole, come per esempio quella provinciale, dove sussistono probabilmente condizioni di maggior omogeneità dei fattori che influenzano il fenomeno di diffusione del virus. Alcune caratteristiche delle curve delle diverse province potrebbero scomparire cumulando le curve per ottenere quella a livello regionale.
Ci rendiamo conto che ci sono dei problemi legati ai dati misurati, specialmente in questo periodo dove in alcune povince la situazione negli ospedali è molto critica a causa dell’elevato numero di pazienti e della carenza di risorse umane a disposizione. Infatti alcuni medici e infermieri sono stati contagiati dal virus e si sono ammalati. Tra le variabili considerate, il numero dei morti presenta anche la difficoltà legata alla sua definizione. Alcuni criticano l’inclusione nel computo dei morti di quelle persone morte e positive al test che presentavano co-morbilità, tipicamente di età avanzata, poiché pensano che sarebbero morte comunque in breve tempo. Questo spiegherebbe almeno in parte l’elevato tasso di mortalità in Italia se confrontato con quello della Cina ad esempio. Si dovrebbe a mio avviso innanzi tutto fare il tampone a tutte le persone morte, cosa che non accade. Questo comunque è comprensibile in una situazione di grande difficoltà a gestire un elevato numero di pazienti. Nel caso di morte con tampone positivo, si potrebbe attribuire la morte al coronavirus se vale almeno una delle due condizioni:
- il tempo tra la diagnosi o l’inizio della fase di peggioramento e la morte è significativamente più piccolo dell’aspettativa di vita della categoria a cui appartiene quel determinato paziente;
- la morte è avvenuta in seguito a complicazioni caratteristiche della malattia indotta dal coronavirus, tipicamente la polmonite.
In questo modo non risolveremmo tutti i casi, ma sarebbe molto meglio che considerare morti per il coronavirus tutti i positivi al test o in alternativa solo i soggetti senza co-morbilità. Vale comunque l’affermazione di prima circa la scala di priorità in una fase di emergenza come quella attuale nelle province più colpite. Inoltre penso che il confronto della mortalità tra situazioni diverse, come il caso cinese e quello italiano, ha senso solo alla fine dell’epidemia e non durante il suo sviluppo a causa del ritardo delle morti. Infine, il tasso di morte potrebbe essere sovrastimato anche a causa della sottostima del numero di contagiati in relazione alla presenza dei portatori sani, dei quali ignoriamo il numero.
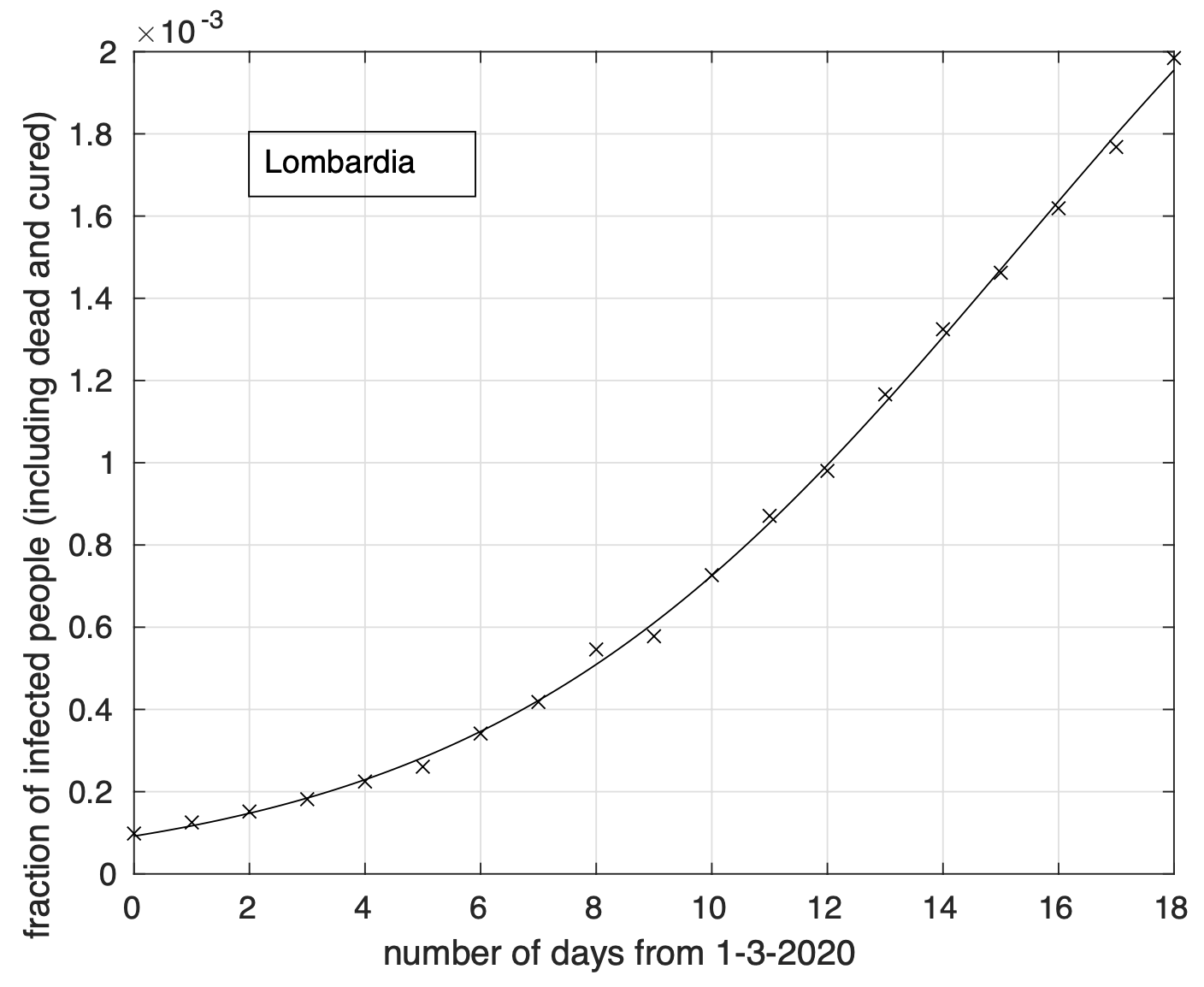
Figura 1. Frazione del numero di contagiati osservati in Lombardia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello logistico è sovrapposto ai dati.
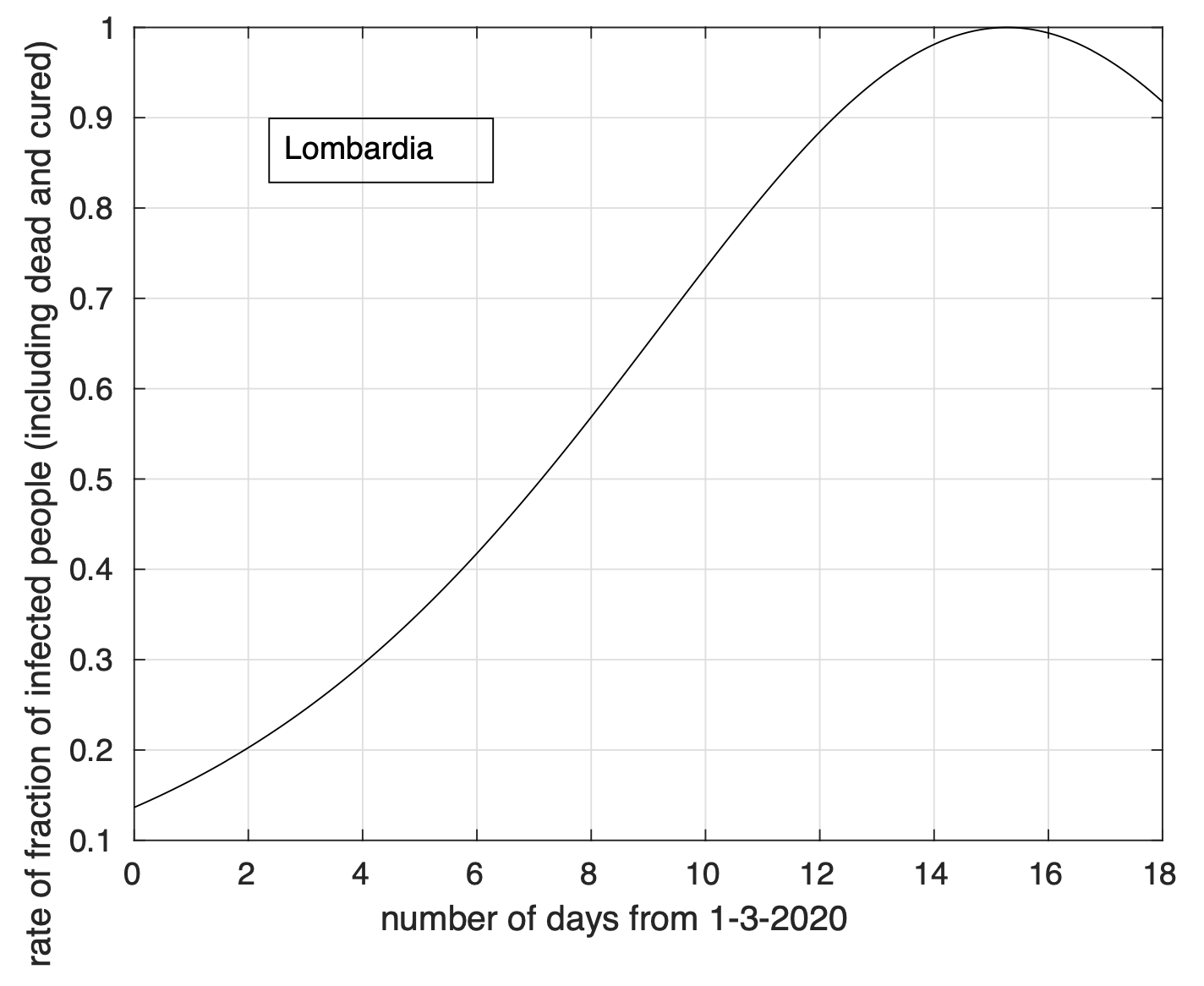
Figura 2. Tasso di crescita della frazione del numero di contagiati osservati in Lombardia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. La curva rappresentata è la derivata del modello teorico sovrapposto ai dati in figura 1.
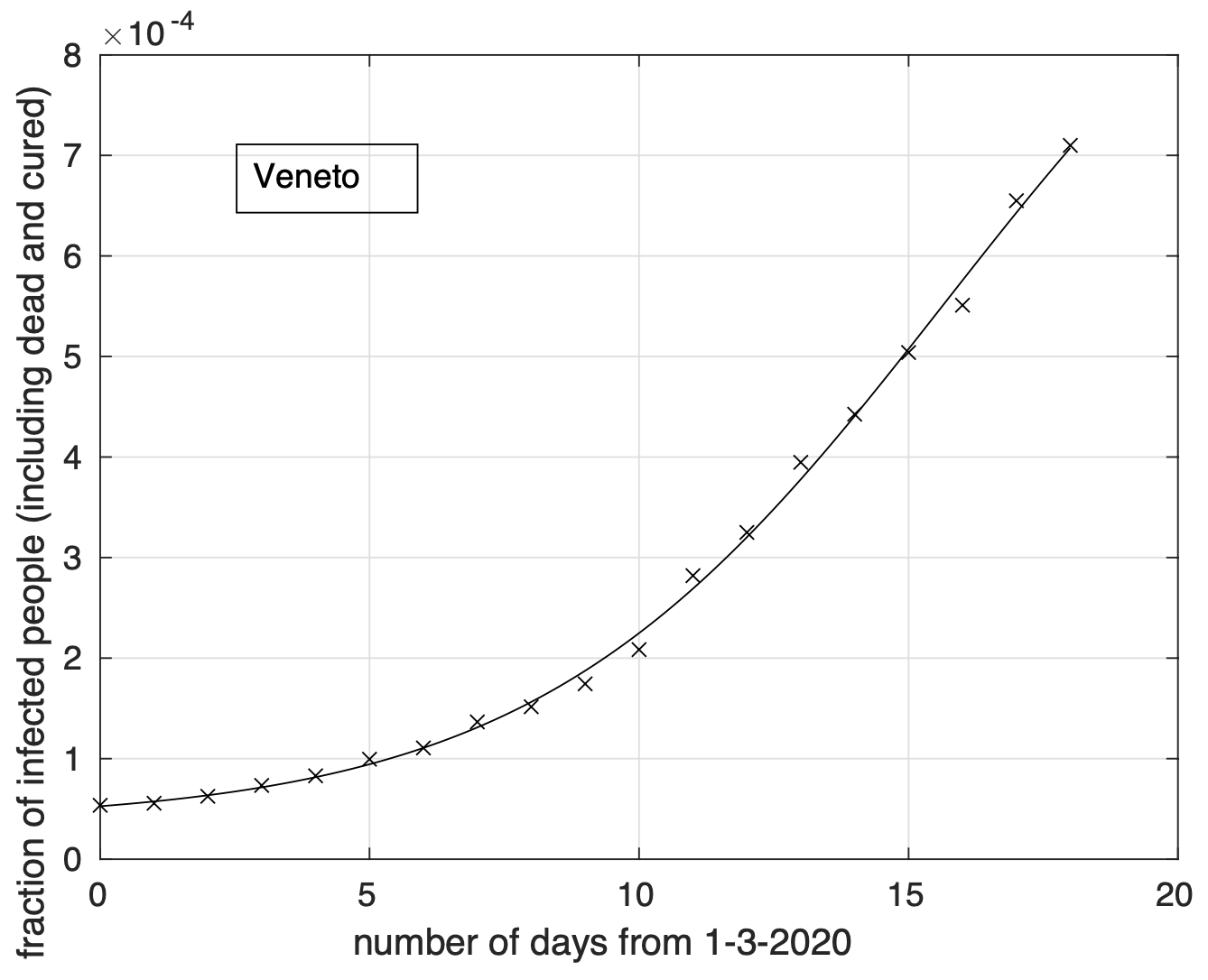
Figura 3. Frazione del numero di contagiati osservati nel Veneto rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello logistico è sovrapposto ai dati.
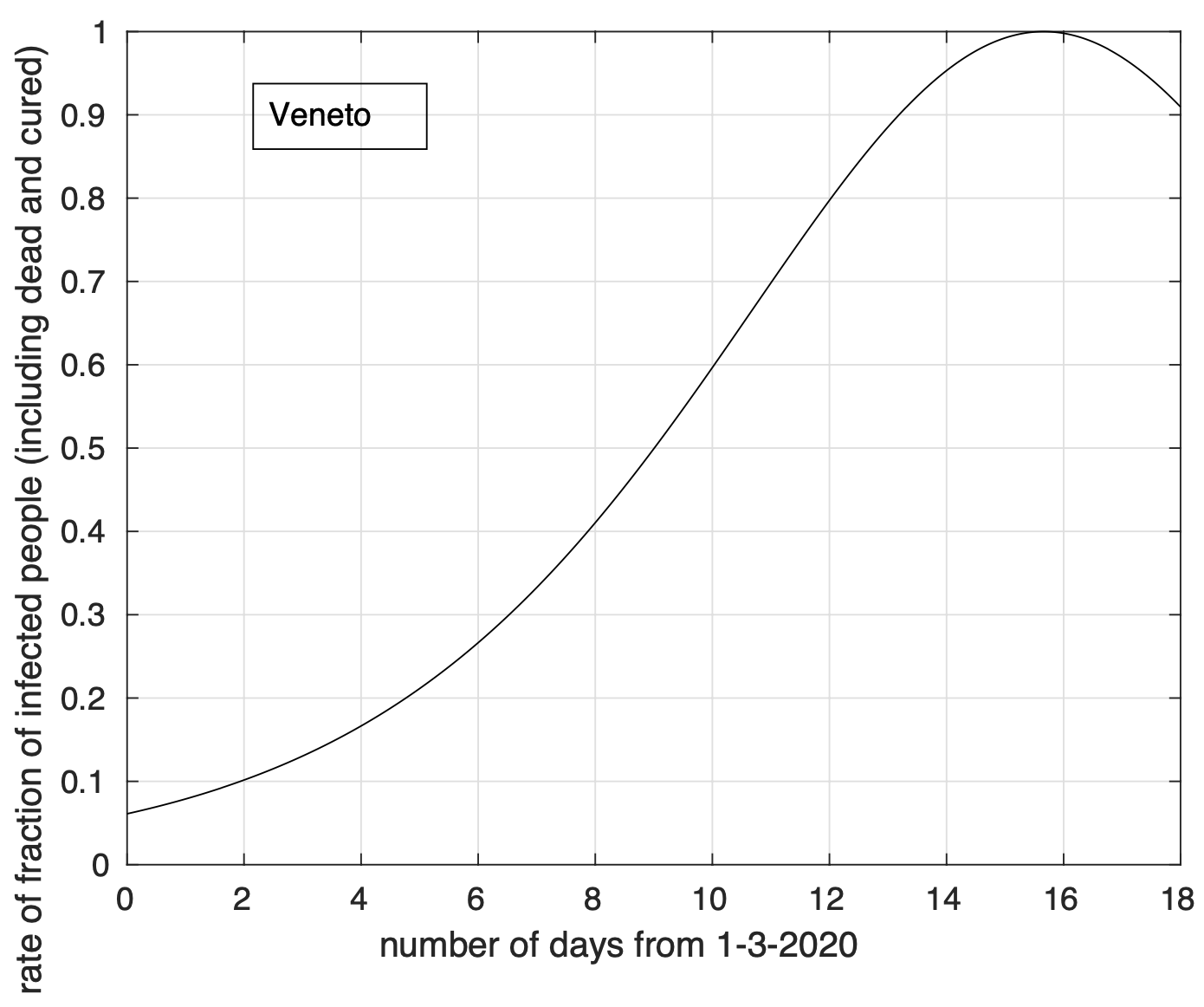
Figura 4. Tasso di crescita della frazione del numero di contagiati osservati in Veneto rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il modello teorico adottato è quello logistico.
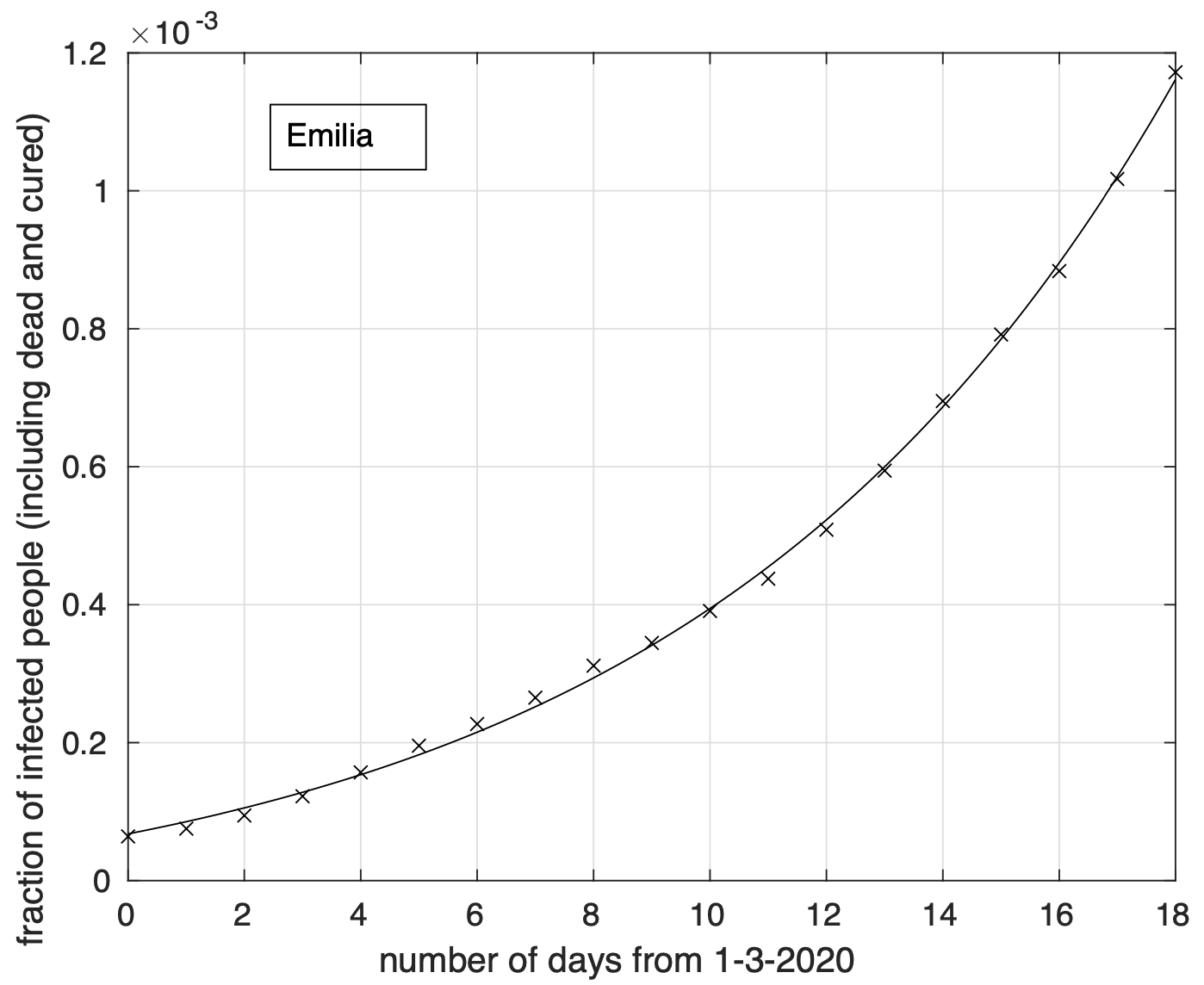
Figura 5. Frazione del numero di contagiati osservati in Emilia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello logistico è sovrapposto ai dati.
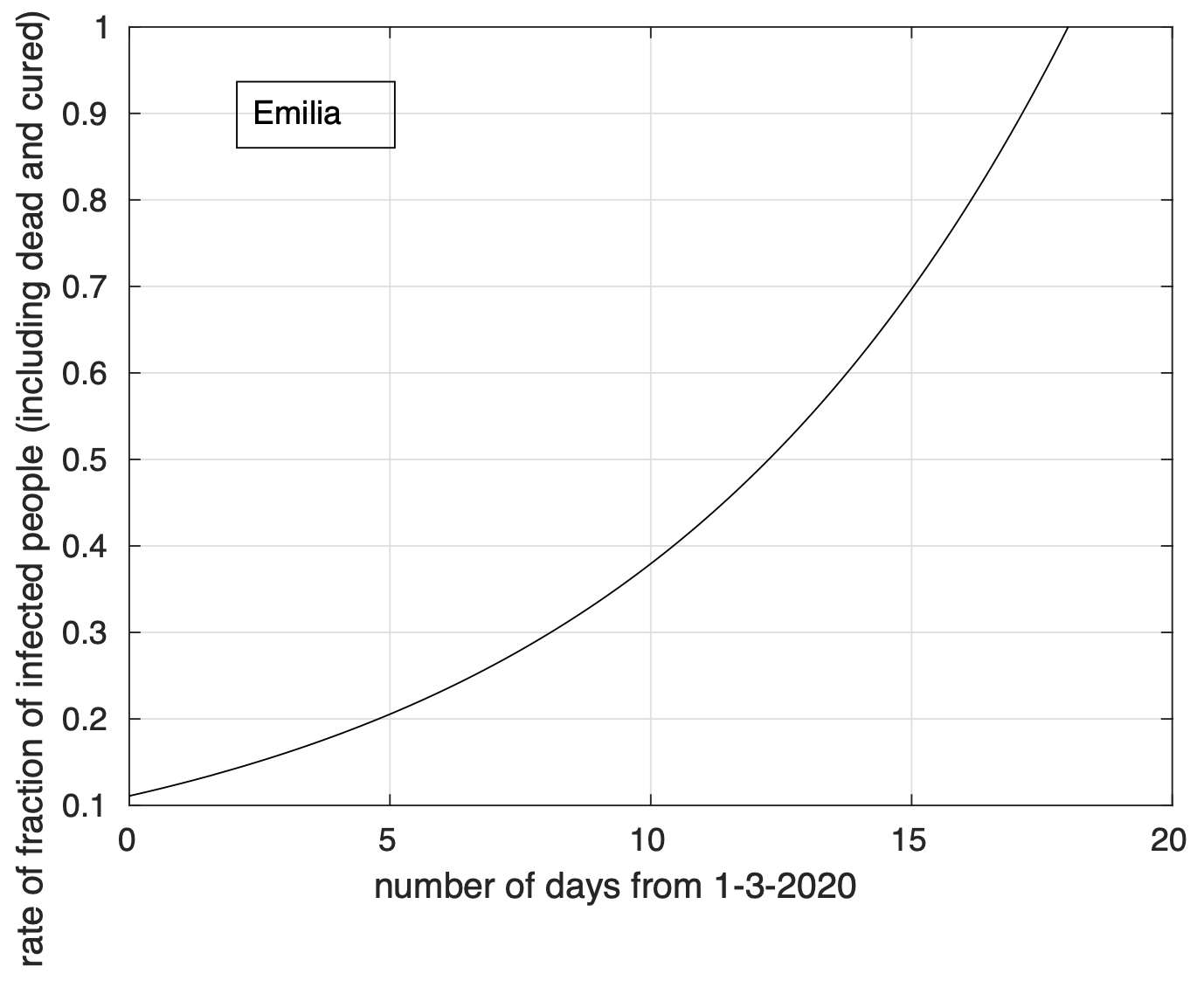
Figura 6. Tasso di crescita della frazione del numero di contagiati osservati in Emilia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il modello teorico adottato è quello logistico.

Figura 7. Frazione del numero di contagiati osservati in Emilia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello doppio logistico è sovrapposto ai dati.
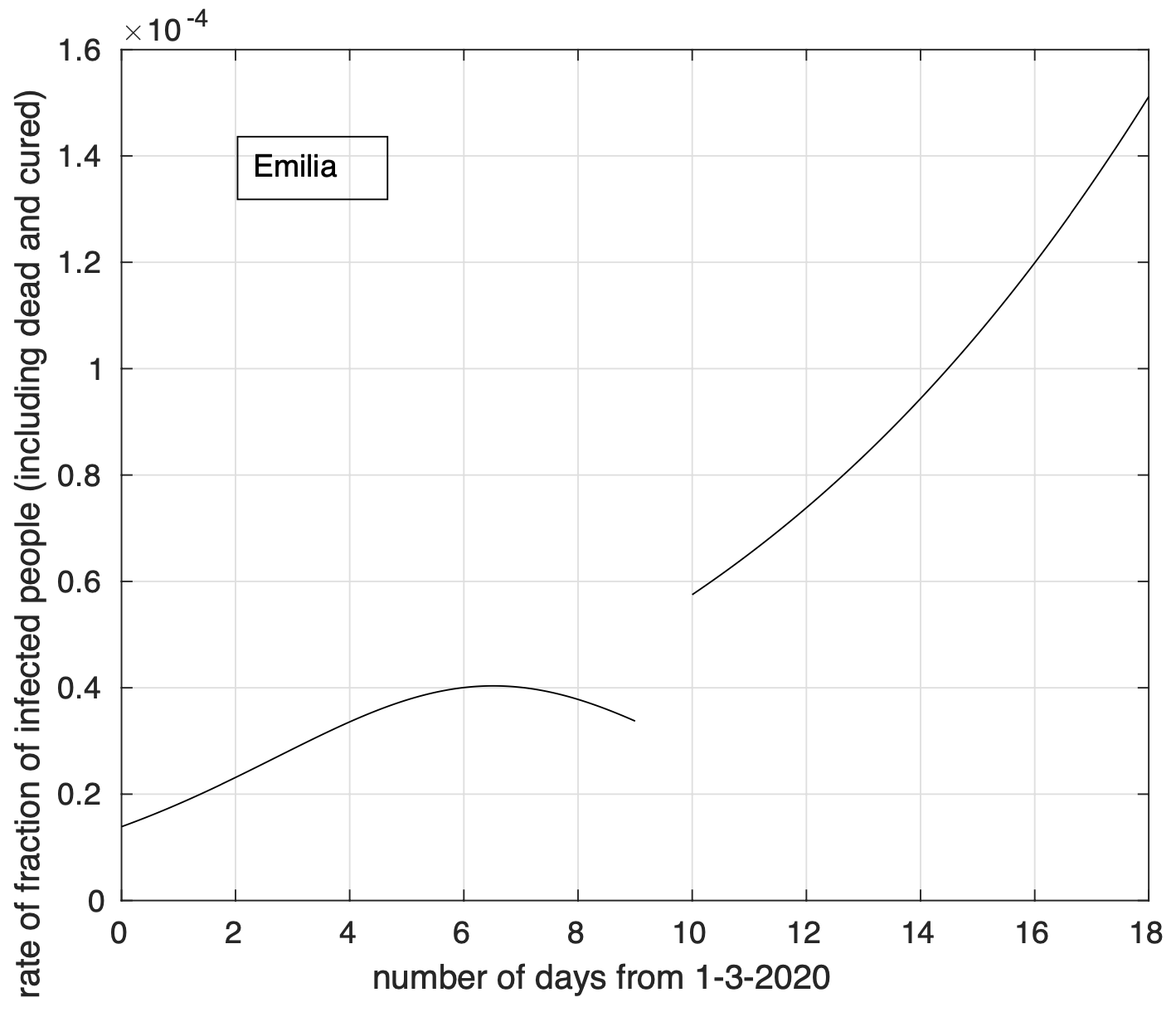
Figura 8. Tasso di crescita della frazione del numero di contagiati osservati in Emilia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il modello teorico adottato è quello doppio logistico.
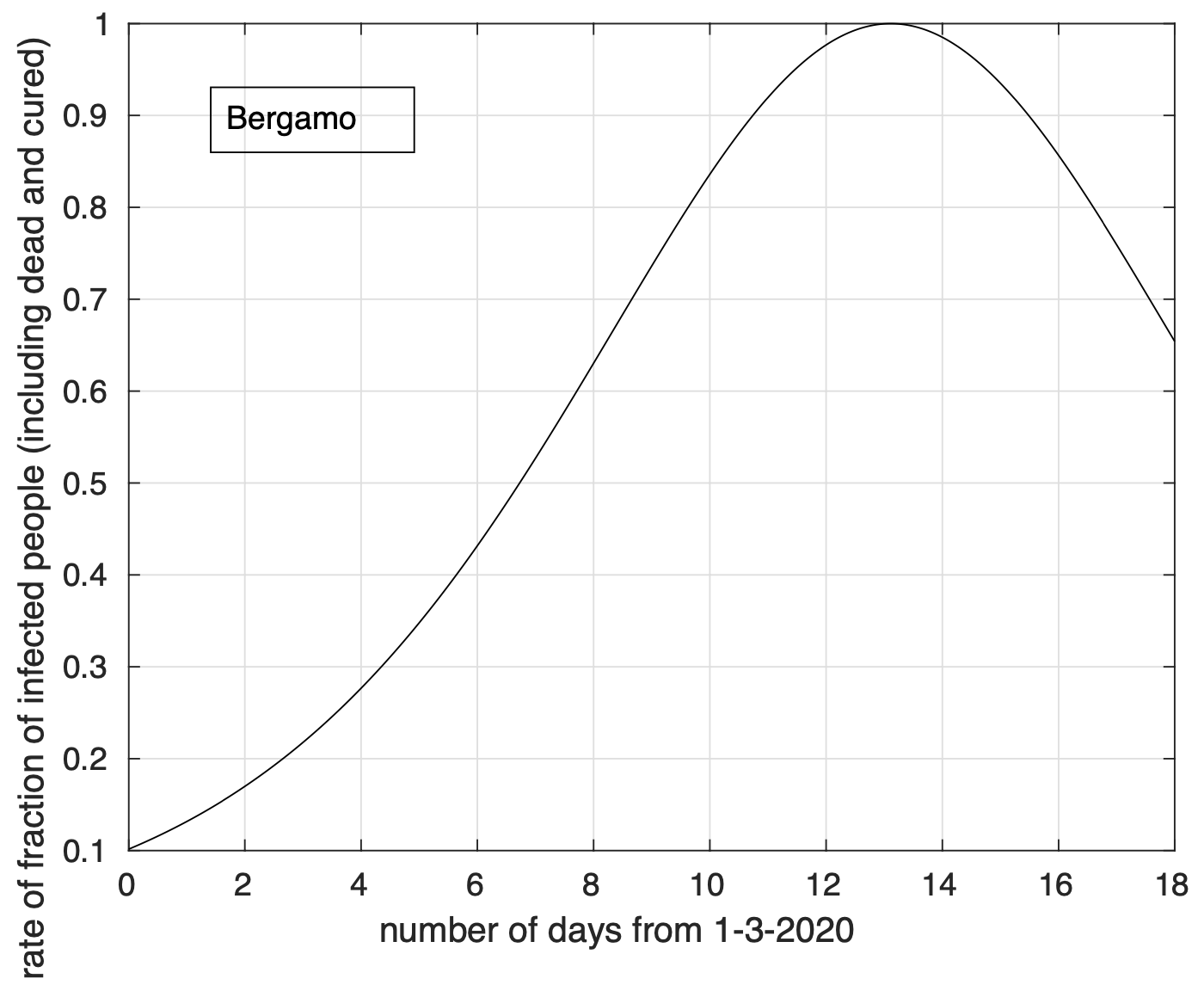
Figura 9. Tasso di crescita della frazione del numero di contagiati osservati a Bergamo rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il modello teorico adottato è quello logistico.
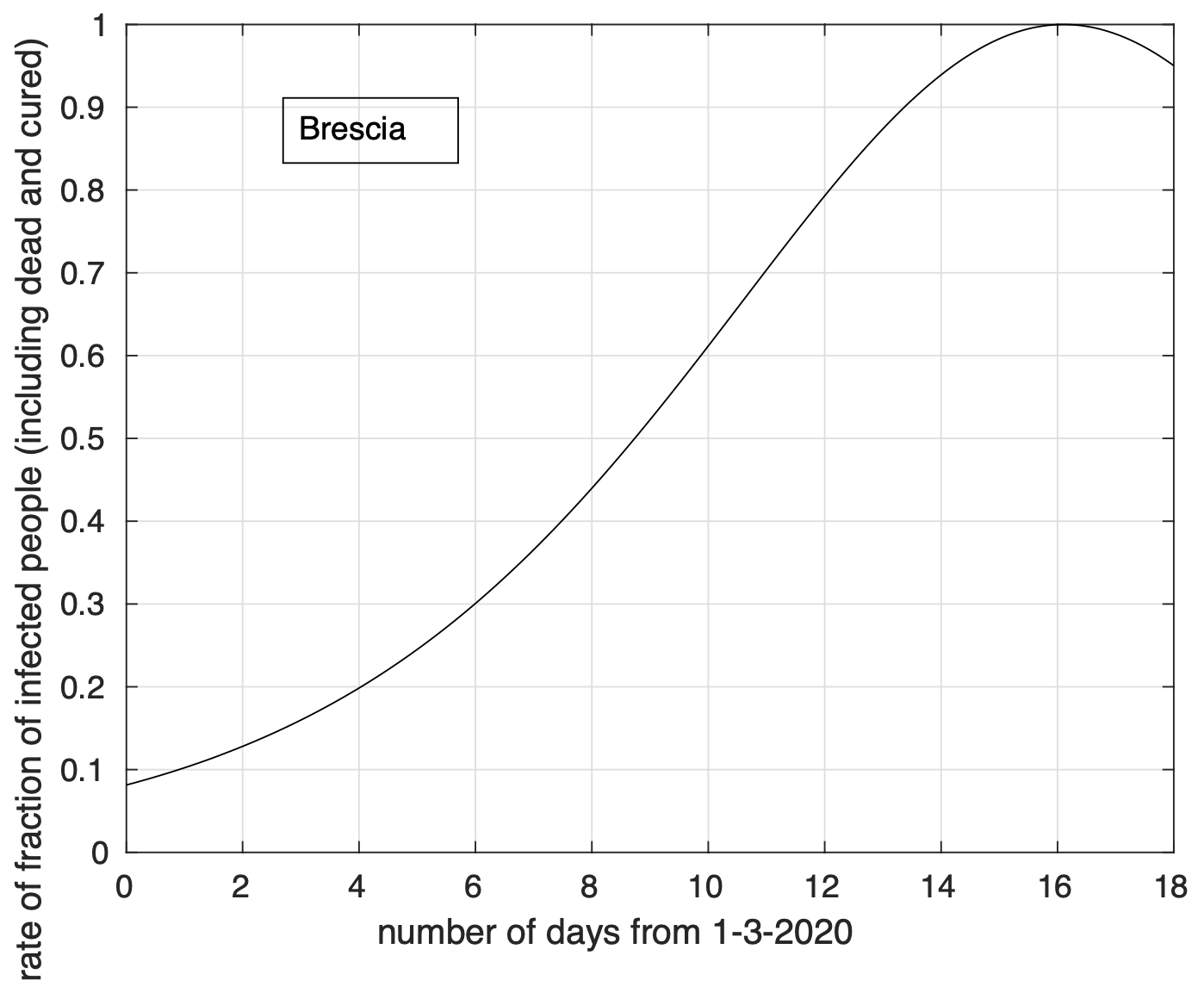
Figura 10. Tasso di crescita della frazione del numero di contagiati osservati a Brescia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il modello teorico adottato è quello logistico.
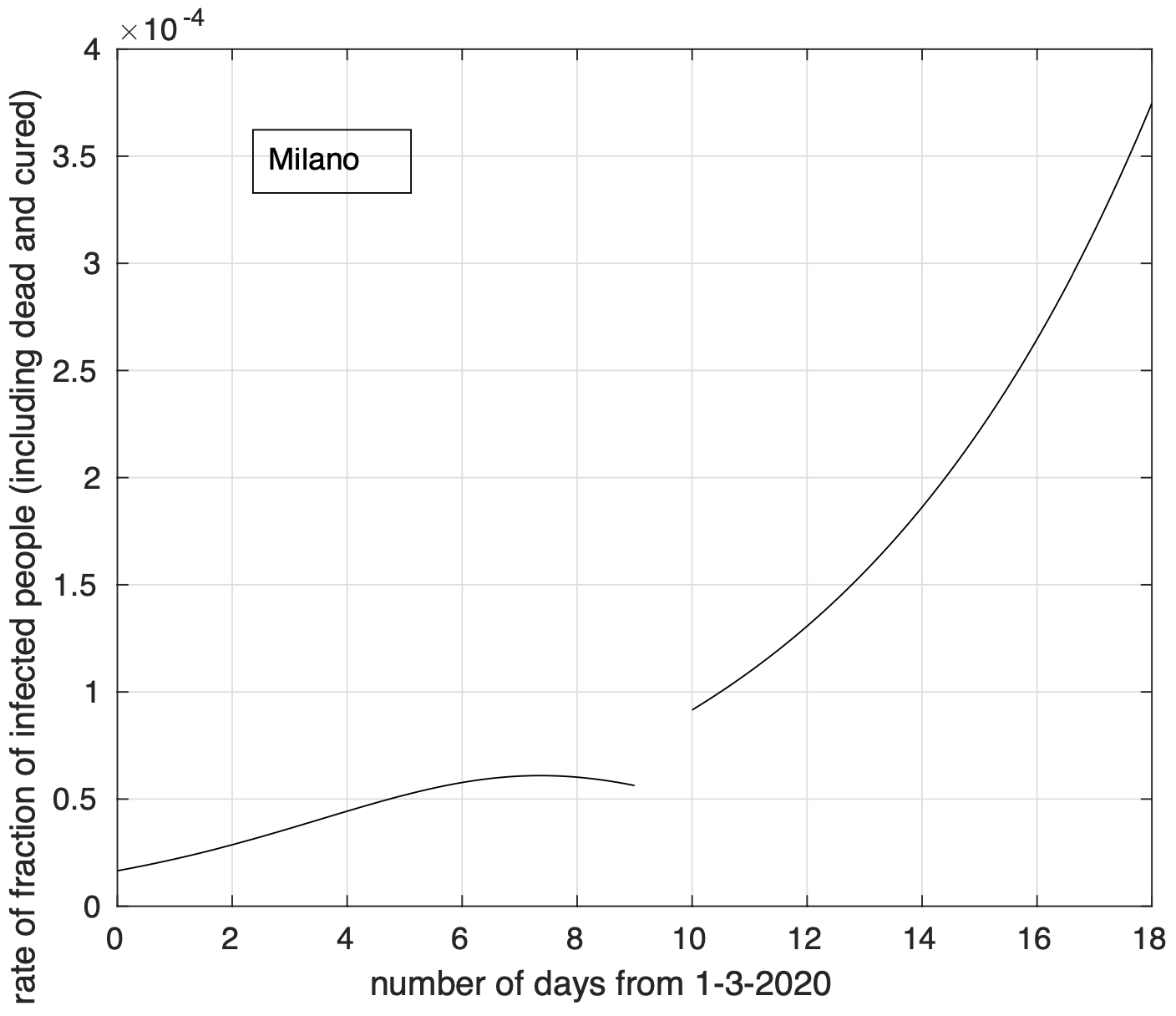
Figura 11. Tasso di crescita della frazione del numero di contagiati osservati a Milano rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il modello teorico adottato è quello doppio logistico.
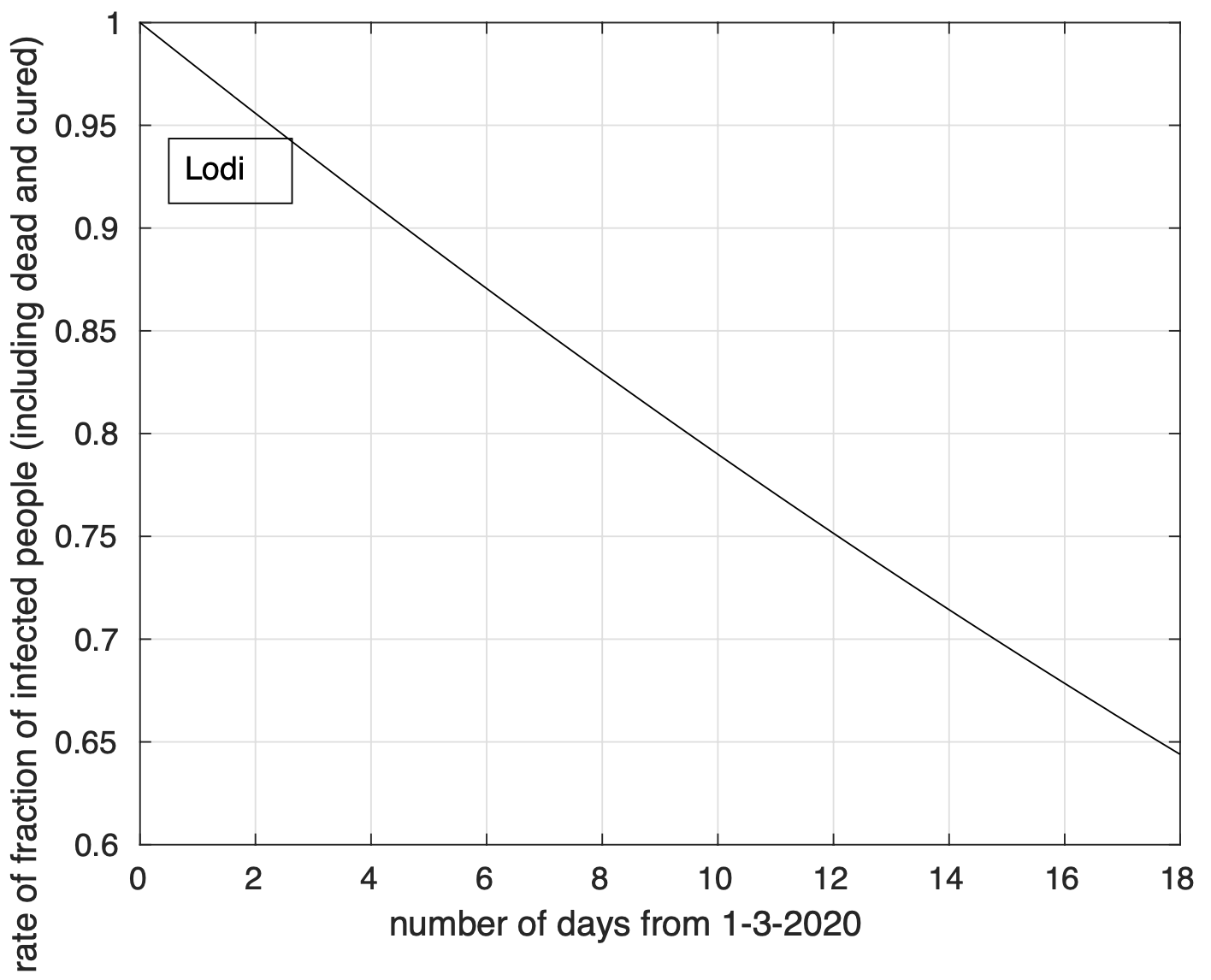
Figura 12. Tasso di crescita della frazione del numero di contagiati osservati a Lodi rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il modello teorico adottato è quello logistico.
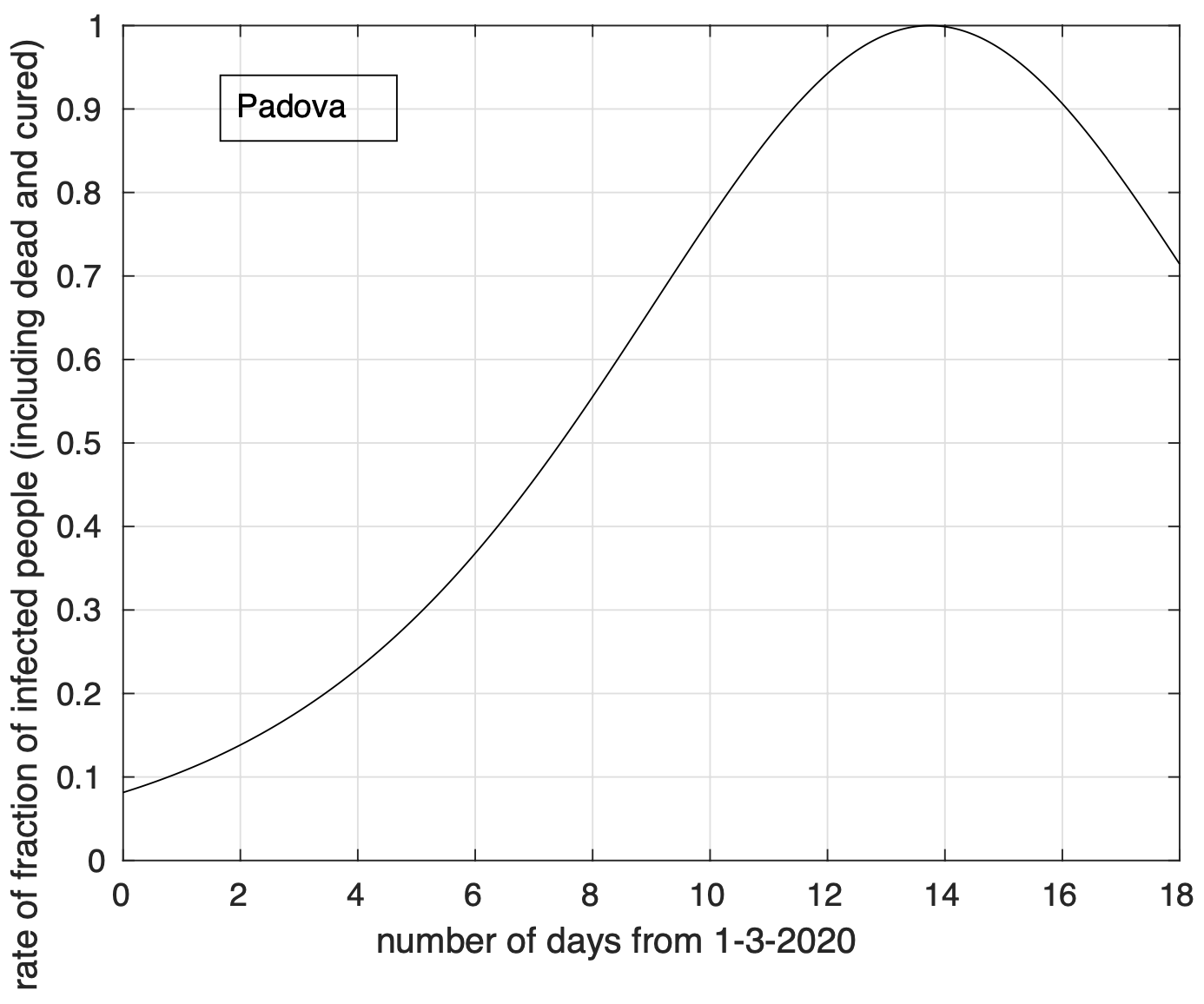
Figura 13. Tasso di crescita della frazione del numero di contagiati osservati a Padova rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il modello teorico adottato è quello logistico.
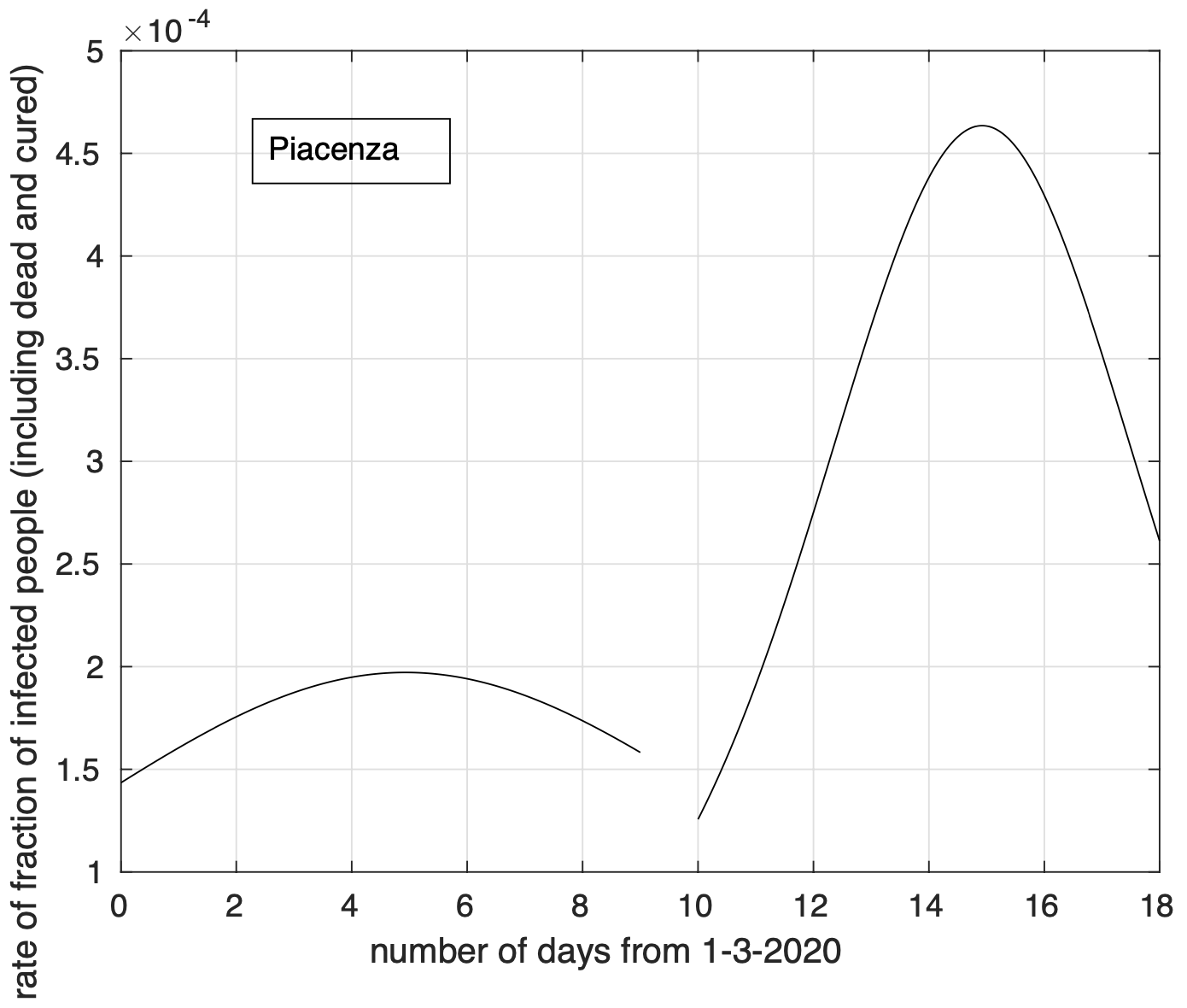
Figura 14. Tasso di crescita della frazione del numero di contagiati osservati a Piacenza rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il modello teorico adottato è quello doppio logistico.
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche
