La geometria dell'origami

L'origami, l'antica arte giapponese del piegare la carta, ha da sempre suscitato interesse da parte dei matematici. La rigidità del materiale, infatti, impone forti limiti al tipo di forme che possono essere create senza tagliare o incollare un foglio di carta. La capacità di creare forme artisticamente interessanti, proprio in virtù di questo vincolo, va di pari passo con la capacità di esplorare e comprendere le regole di piegatura.

Nella letteratura scientifica, contrariamente a quanto si può pensare, esiste una notevole quantità di studi sugli origami. La maggior parte di questi può essere catalogata nell'ambito dell'algebra, della geometria o della teoria degli algoritmi. In queste trattazioni la definizione matematica di origami passa attraverso una descrizione combinatoria delle pieghe a cui viene sottoposto il foglio di carta.

Recentemente, in una collaborazione con Bernard Dacorogna (Ecole Polytechnique Fédérale de Lausanne) e Paolo Marcellini (Università di Firenze) riguardante la ricerca di soluzioni ad un particolare sistema di equazioni differenziali, ci siamo involontariamente trovati di fronte a quella che potrebbe essere interpretata come una definizione analitica di origami. 

Un origami può essere infatti identificato dalla funzione che lega i punti del foglio non piegato ai punti corrispondenti del modello piegato.

In sostanza, si tratta di una funzione che parte da punti appartenenti a una regione del piano (tipicamente un rettangolo) e arriva in punti dello spazio (in questo modo abbiamo schematizzato la proprietà degli origami di essere oggetti bidimensionali immersi nello spazio tridimensionale). Per catturare le proprietà di rigidità della carta (allo stesso modo, con quanto detto finora, potremmo rappresentare una superficie elastica, una pellicola di sapone, un tessuto, eccetera) usiamo una condizione analiticamente molto semplice: il differenziale della funzione deve essere una isometria.

Cioè, potremmo dire che la funzione che rappresenta l'origami deve essere, almeno in ogni punto isolatamente, se non nella sua totalità, quella che in matematica viene chiamata isometria. Un'isometria può essere "lineare", cioè un movimento nello spazio che si ottiene combinando insieme rotazioni, traslazioni e simmetrie oppure "non lineare", ossia un movimento simile a quello che si effettua quando, ad esempio, si curva un foglio per formare un cono.

Per i più "esperti" in matematica: questa condizione si può equivalentemente esprimere dicendo che la matrice gradiente (una matrice 3x2) è ortogonale. In realtà non vogliamo però richiedere che la funzione sia ovunque differenziabile. Si capisce infatti che i punti in cui il foglio viene piegato sono proprio punti di non differenziabilità per la funzione. Si può quindi definire un origami matematico come una funzione lipschitziana (in particolare continua) con quasi ovunque derivata ortogonale.;

La definizione così data risulta molto generale, rispetto alle usuali definizione combinatorie. Prima di tutto perché questa definizione tiene conto della possibilità di avere delle parti curve. In effetti se la funzione è regolare il foglio non ha nessuna piega, ma potrebbe essere incurvato nello spazio. La superficie risultante ha la proprietà di essere una superficie rigata. E’ anche possibile avere la coesistenza di parti curve e di pieghe e in tal caso è anche possibile ottenere pieghe curve. Se si traccia una curva su un foglio di carta e si prova a piegare il foglio lungo tale curva si otterrà facilmente una superficie rigata con una linea di singolarità, ovvero un insieme di punti in cui non è definito il piano tangente.

Un altro vantaggio di questa definizione analitica è che non richiede una particolare struttura nell'insieme delle singolarità. In particolare si tiene in considerazione la possibilità di avere origami originati da una quantità infinita di pieghe. Questa particolarità permette ad esempio di trattare origami frattali, in cui l'insieme delle pieghe si accumula sul bordo del foglio di carta; Infine la definizione non è ristretta al caso di fogli bidimensionali nello spazio. La stessa identica definizione ci permette di definire le pieghe di fogli tridimensionali o n-dimensionali.

Come riferimento rimandiamo al recente articolo: 

Dacorogna -- Marcellini -- Paolini: Origami and Partila   Differential Equations, Notices of the American Math. Soc., May 2010. 

Figura 1

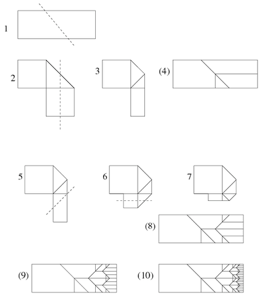
In questa figura è rappresentato un esempio di origami frattale. Piegando ripetutamente una striscia di carta e assottigliandola, si ottiene una forma a spirale (7). Se si riapre il foglio, si vedranno impresse le linee di piegatura (ovvero le singolarità della funzione), che formano una struttura frattale ricorsiva (10).

Figura 2

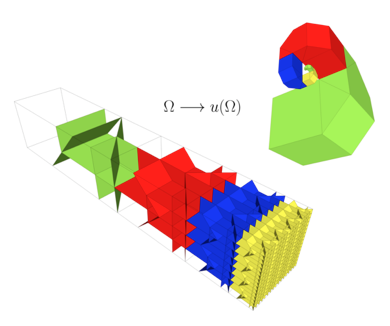
In questa figura è rappresentato  l'analogo della figura precedente in tre dimensioni. In basso a sinistra è rappresentato il foglio tridimensionale (ovvero un parallelepipedo) sul quale sono state disegnate le pieghe. In alto a destra è rappresentato l'origami risultante che ha la forma di una spirale spaziale, che si assottiglia sempre di più. 

Figura 3

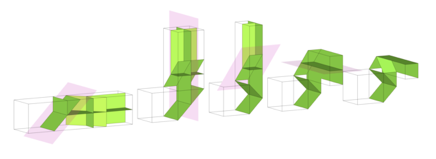
In questo diagramma è rappresentata una delle iterazioni nella costruzione frattale descritta nella figura precedente. La prima iterazione si ottiene infatti da una successione di 4 pieghe lungo i piani colorati in rosa. Immaginando di riaprire il foglio dopo la piegatura, si ritroveranno impresse le pieghe sulla regione poligonale colorata in verde.