La sequenza del numero totale dei contagiati osservati di Covid-19 in Italia presenta piccole ma visibili deviazioni non casuali dei dati dal modello teorico adottato dopo la fine della fase evolutiva iniziale di tipo esponenziale, come illustrato in figura 1.
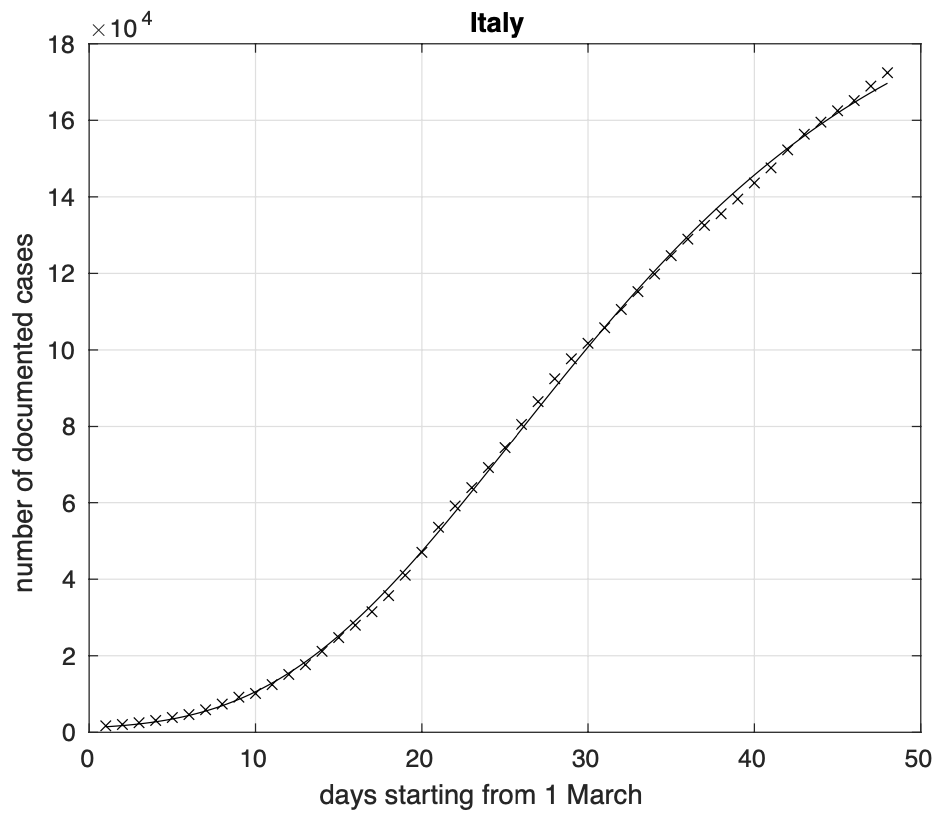
Figura 1. Sequenza del numero dei contagiati osservati in Italia. Il miglior fit con un modello logistico generalizzato è sovrapposto ai dati.
Il modello teorico attuale è stato da noi ottenuto generalizzando quello logistico tramite l’introduzione di un quarto parametro che permette di avere la crescita iniziale e quella finale con velocità diverse tra loro. Abbiamo optato per questa scelta invece di adottare altri modelli come quello di Gompertz, contenente anch’esso quattro parametri, perchè il quarto parametro ha nel nostro caso una chiara interpretazione. Come si può vedere confrontando la figura 2 relativa al modello logistico, con la precedente, relativa alla sua generalizzazione, si nota che il nuovo modello si adatta meglio ai dati.
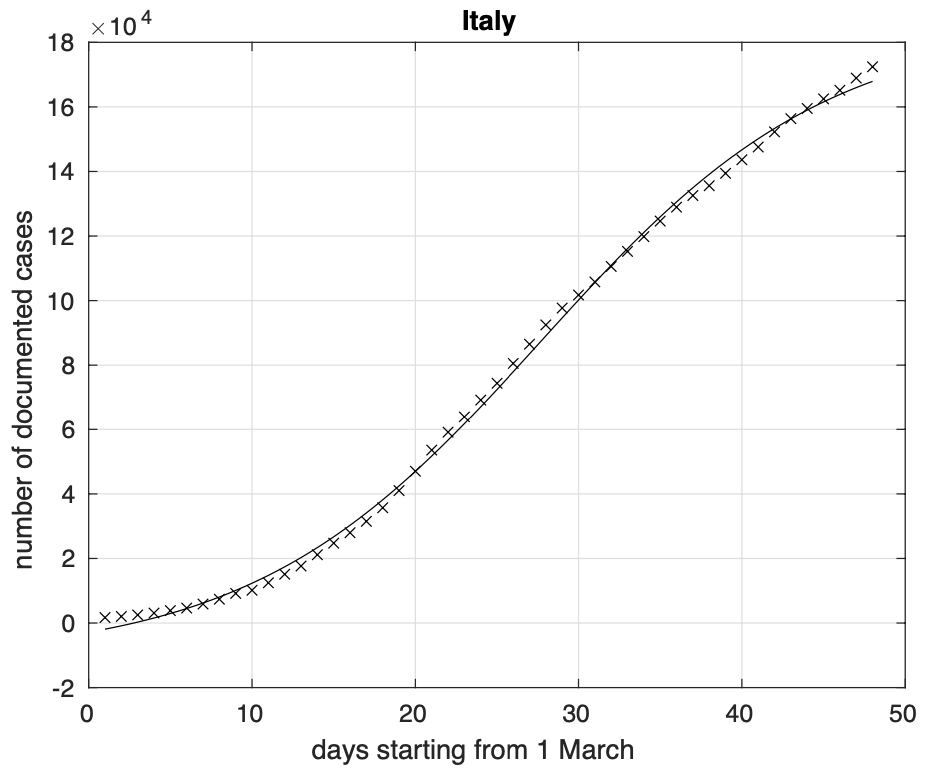
Figura 2. Sequenza del numero dei contagiati osservati in Italia. Il miglior fit con un modello logistico è sovrapposto ai dati.
Tornando allo scostamento, notiamo che aumenta a mano a mano che passa il tempo ed anche muovendoci dal livello nazionale a quello regionale (vedi figura 3) e poi a quello provinciale (vedi figura 4).
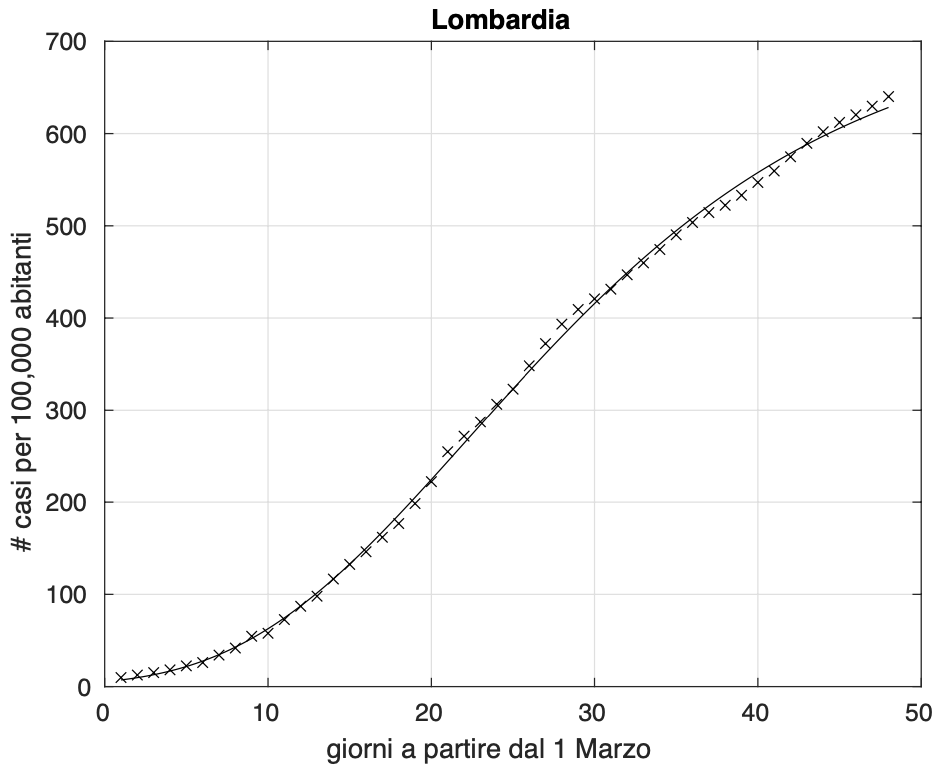
Figura 3. Sequenza del numero dei contagiati osservati in Lombardia. Il miglior fit con un modello logistico generalizzato è sovrapposto ai dati.
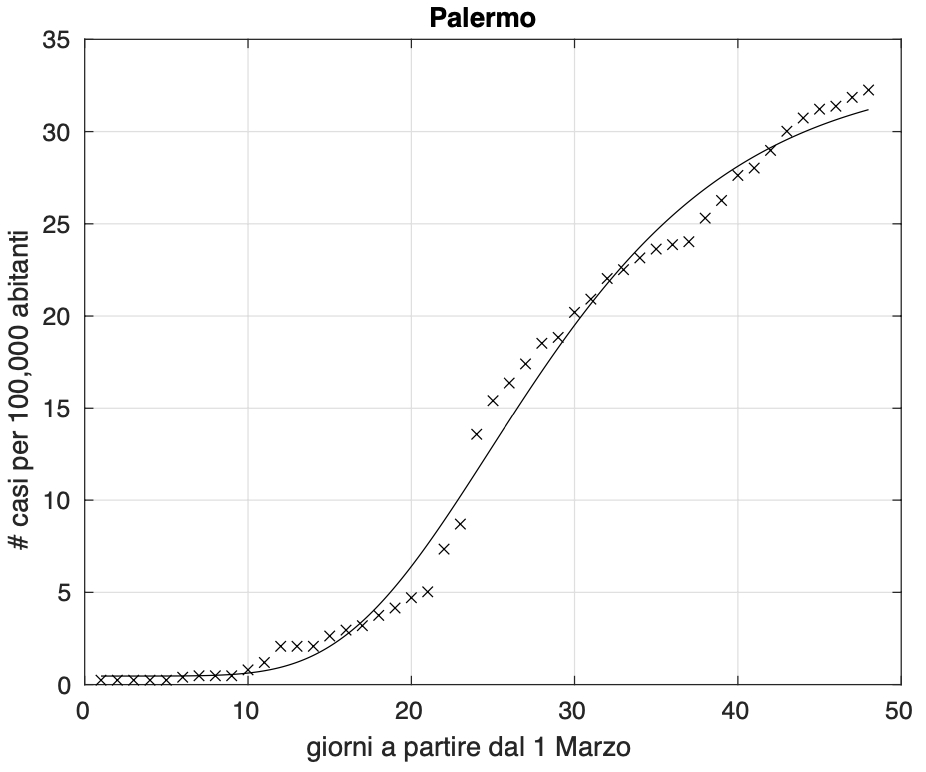
Figura 4. Sequenza del numero dei contagiati osservati nella provincia di Palermo. Il miglior fit con un modello logistico generalizzato è sovrapposto ai dati.
Comunque, le deviazioni sono a volte minime, come nel caso della provincia di Pavia (vedi figura 5).
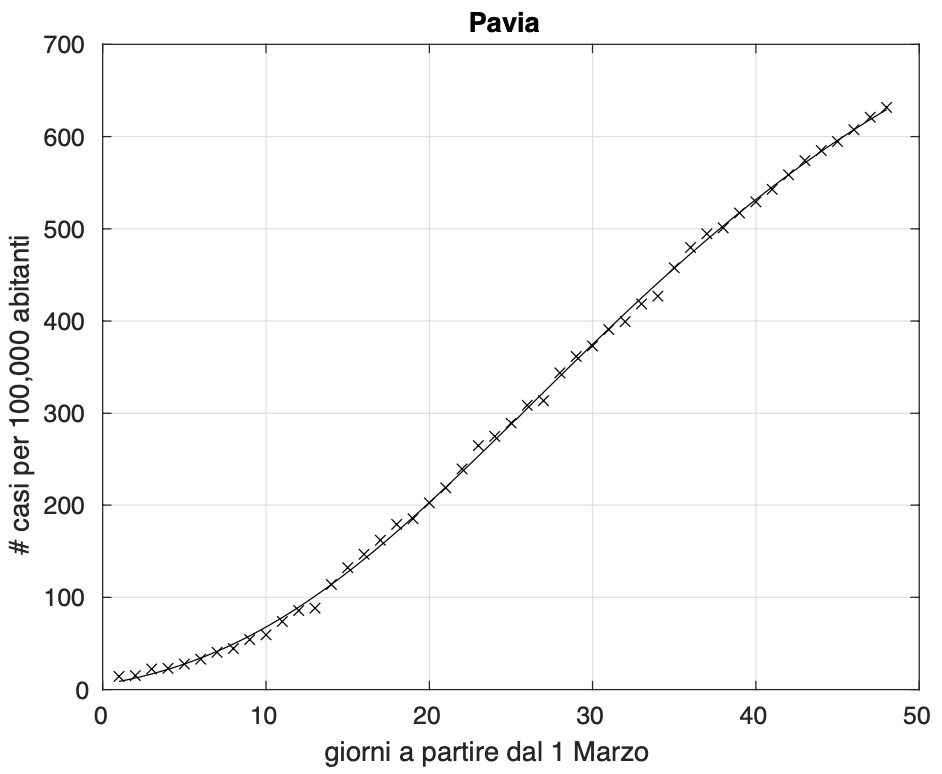
Figura 5. Sequenza del numero dei contagiati osservati nella provincia di Pavia. Il miglior fit con un modello logistico generalizzato è sovrapposto ai dati.
Si possono inoltre avere altri due tipi di deviazioni dei quali conosciamo le cause, legate ai test con i tamponi utilizzati per diagnosticare i contagiati osservati. In entrambi i casi, la deviazione consiste in un aumento molto grande del numero totale dei contagiati osservati rispetto al giorno precedente. In un caso questo si spiega col prelievo contemporaneo in uno stesso giorno di un insieme di decine o centinaia di tamponi da residenze sanitarie con un’elevata percentuale di contagiati, come avvenuto ad esempo a Catanzaro verso la fine di marzo (vedi figura 6).
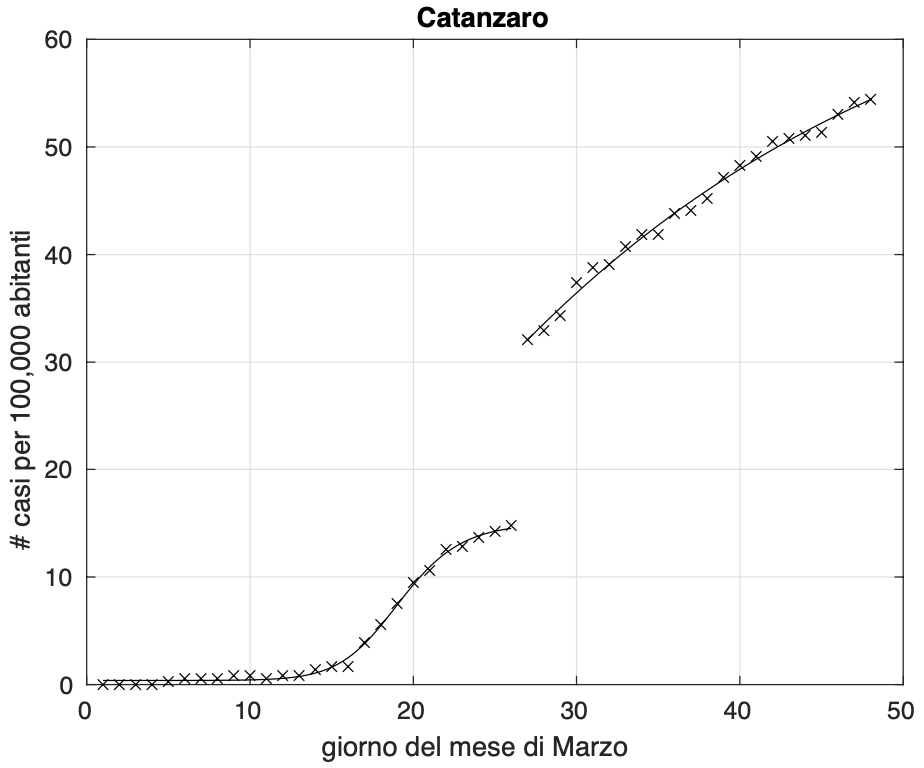
Figura 6. Sequenza del numero dei contagiati osservati nella provincia di Catanzaro. Il miglior fit con un modello logistico generalizzato è sovrapposto ai dati.
Questi tamponi vengono poi analizzati e registrati tutti lo stesso giorno e questo spiega il fenomeno. Nell’altro caso invece gli aumenti si spiegano in termini del considerevole numero di campioni non ancora registrati, che viene a volte riportato all’interno del file con i dati a livello provinciale messo a disposizione dal Dipartimento della Protezione Civile ogni giorno alle 18. Quello che accade è che a volte tanti di questi casi denominati “in fase di definizione”, vengono analizzati e registrati lo stesso giorno (vedi figura 7).
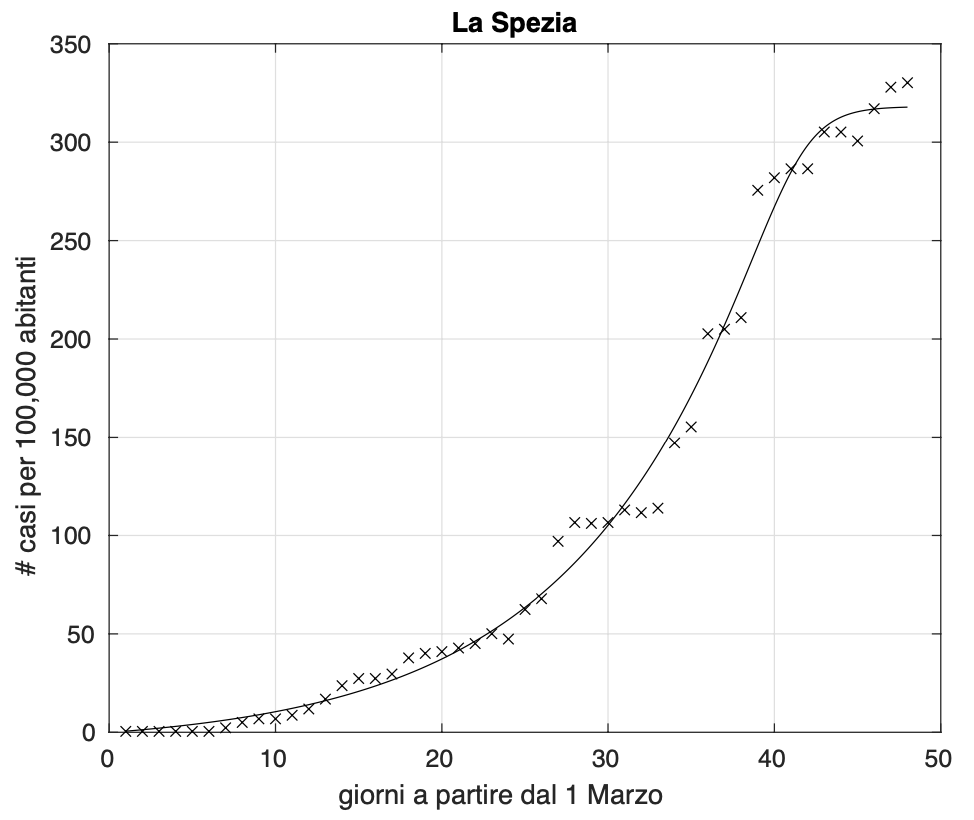
Figura 7. Sequenza del numero dei contagiati osservati nella provincia di La Spezia. Il miglior fit con un modello logistico generalizzato è sovrapposto ai dati.
Notiamo in questo caso anche la presenza di deviazioni legate ad errato conteggio o trascrizione dei casi positivi al test, che possono spiegare il fatto che il numero totale di contagiati in alcuni giorni scenda rispetto al valore del giorno precedente, cosa per definizione impossibile.
Torniamo ora al tipo di deviazioni descritte all’inizio per indagare sulle cause che le generano. Per esse appare evidente la caratteristica di periodicità. Abbiamo subito ipotizzato che la deviazione non riguardasse la reale evoluzione dell’epidemia ma che fosse legata alla misura dei dati sperimentali. La periodicità naturale da considerare è quella settimanale legata all’analisi dei campioni per il test diagnostico. Ci aspettiamo infatti che il numero di test analizzati giornalmente possa essere inferiore nei giorni di fine settimana.
Questo si vede chiaramente nella figura 8, col numero di test analizzati al giorno che cresce a grande scala temporale in modo lineare nel tempo, secondo il segmento tratteggiato, ma con delle variazioni periodiche settimanali di ampiezza anch’essa crescente linearmente col tempo.
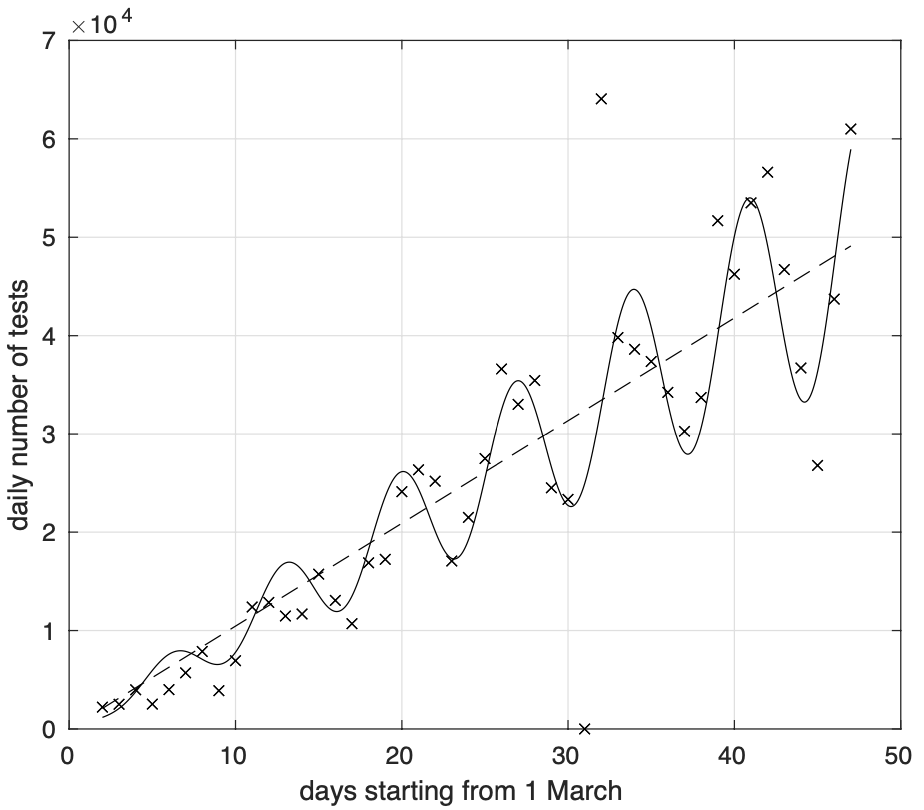
Figura 8. Sequenza del numero giornaliero di test effettuati in Italia per la diagnosi di coronavirus.
Si nota che localmente i valori minimi misurati corrispondono ai lunedì. Probabilmente quindi i risultati registrati ufficialmente e che appaiono un certo giorno sul bollettino della Protezione civile sono relativi ai campioni analizzati il giorno prima o nei giorni precedenti. Avendo a disposizione i dati disaggregati, si potrebbe più correttamente far apparire il giorno del prelievo del campione biologico del paziente. In questo modo, due dei tre tipi di errore scomparirebbero. D’altro canto, per un certo tempo, il numero di nuovi casi “diagnosticati” un fissato giorno probabilmente cambierebbe, ma poi si stabilizzarebbe.
Questa periodicità si riflette sul numero di casi positivi misurato ogni giorno, come illustrato in figura 9, dove viene anche mostrato l’andamento teorico del tasso di crescita del numero totale di positivi derivato dal modello per il numero totale di contagiati osservati stimato a partire dai dati (vedi figura 1).
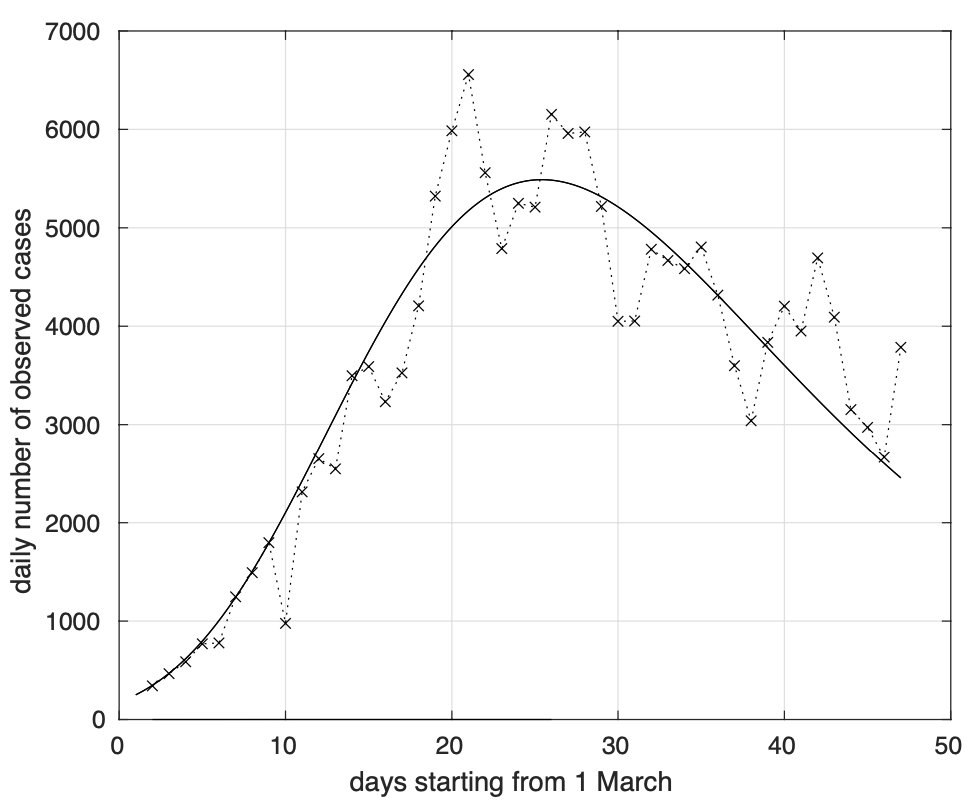
Figura 9. Sequenza del numero giornaliero di contagiati osservati in Italia in seguito alla positività al test. Il modello teorico sovrapposto ai dati è derivato da quello logistico gener- alizzato stimato a partire dalla sequenza dei contagiati osservati in Italia in figura 1.
Nella figura 10 possiamo vedere l’analogo risultato per il modello logistico che mostra un peggior adattamento ai dati nelle code.
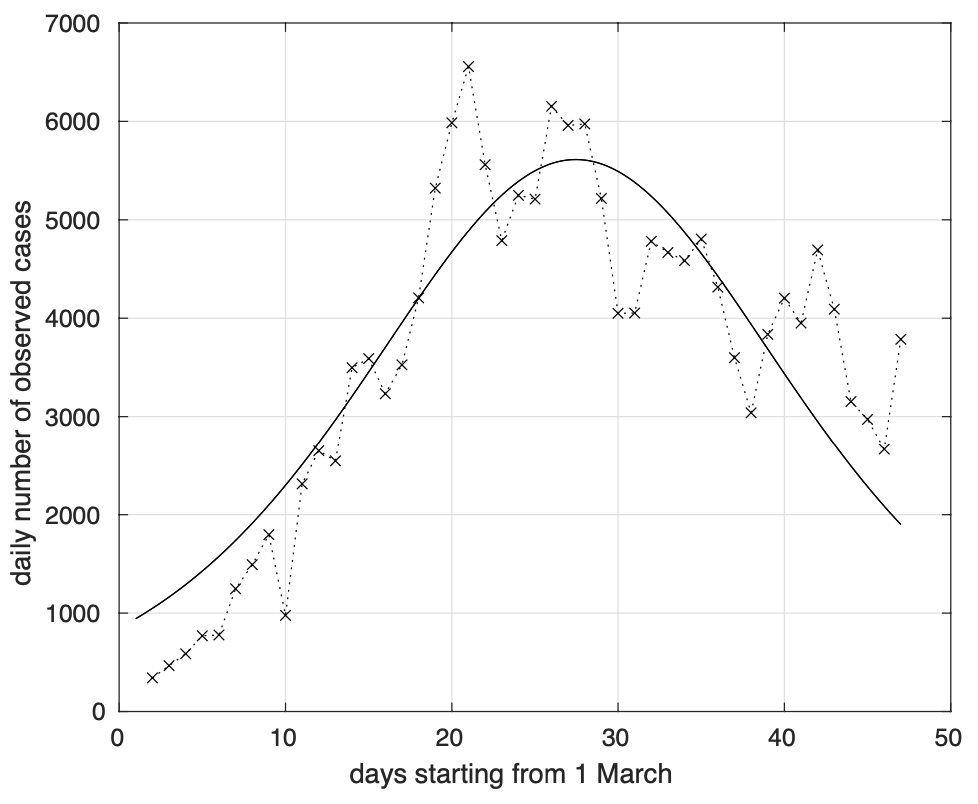
Figura 10. Sequenza del numero giornaliero di contagiati osservati in Italia in seguito alla positività al test. Il modello teorico sovrapposto ai dati è derivato da quello logistico stimato a partire dalla sequenza dei contagiati osservati in Italia in figura 2.
La stima della probabilità nel tempo che un sintomatico risulti positivo per la presenza del coronavirus, ottenuta come rapporto tra il modello teorico stimato per il tasso di crescita in figura 9 ed il numero di test effettuati al giorno depurato della componente additiva periodica in figura 8 viene rappresentata in figura 11.
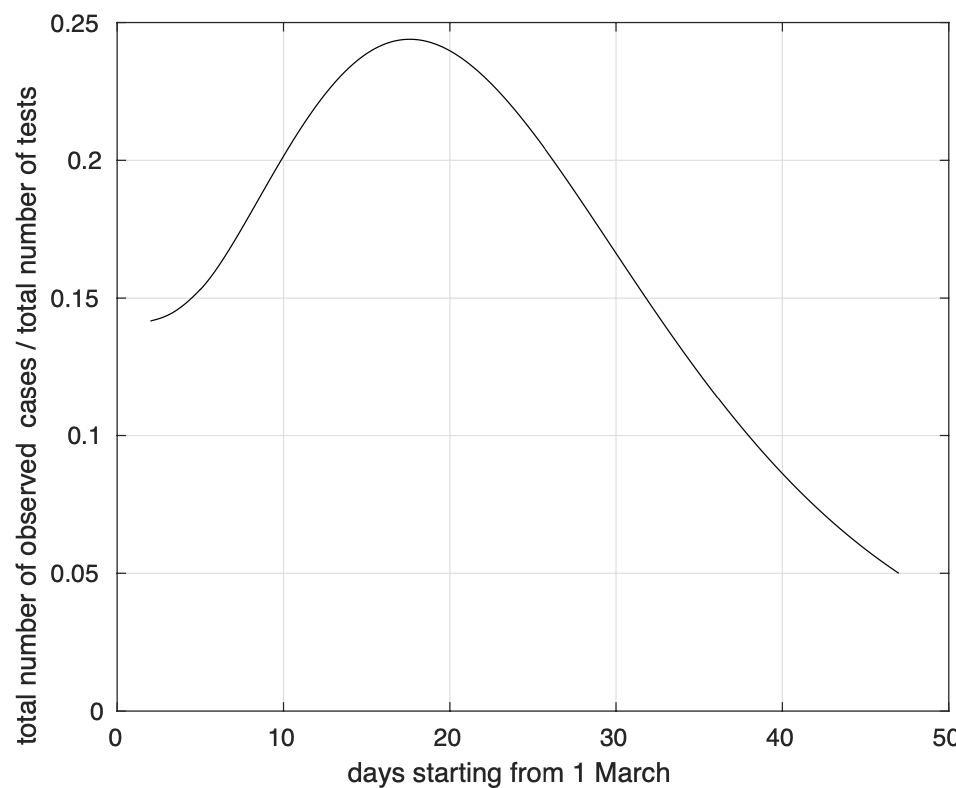
Figura 11. Sequenza della probabilità di test positivo per soggetti sintomatici.
Alla luce del risultato ottenuto, abbiamo modellizzato la deviazione nel tempo tra il modello teorico per il numero totale dei casi ed i dati misurati tramite una componente periodica con ampiezza cresente linearmente nel tempo. Il risultato appare nella figura 12.
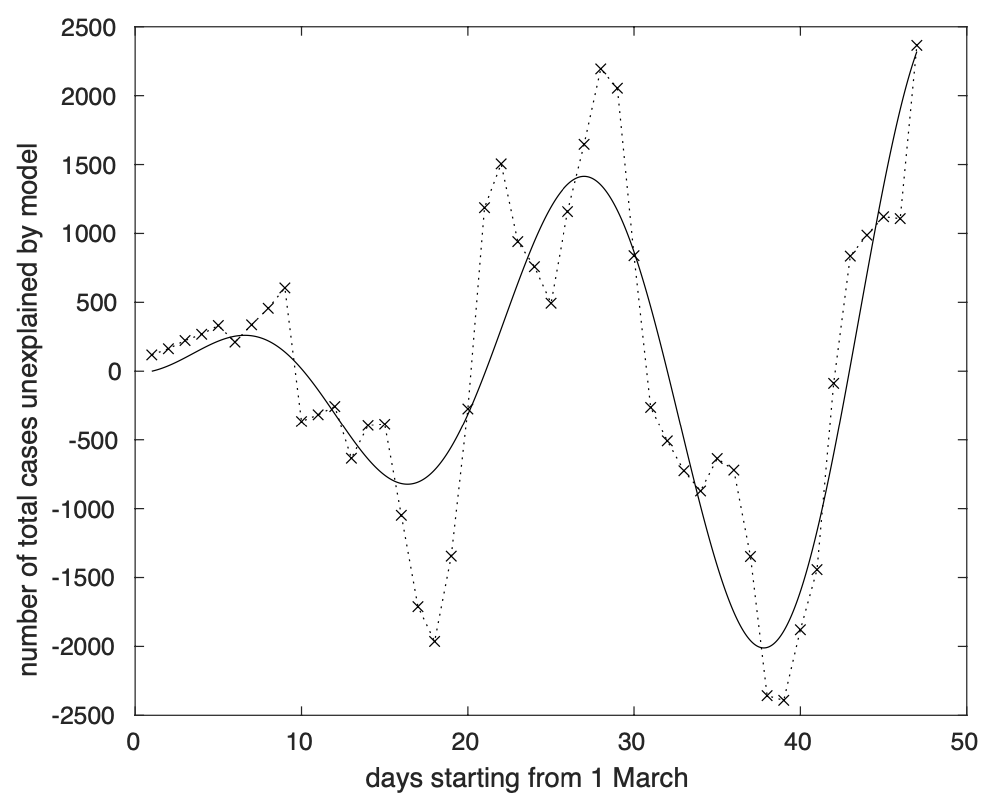
Figura 12. Deviazione della sequenza dei contagiati osservati in Italia dal modello teorico logistico generalizzato rappresentati in figura 1.
Notiamo che il periodo è stavolta poco meno di 22 giorni, quindi vicino a 21 giorni, ossia tre volte quello del numero di test al giorno e del tasso di crescita giornaliero. Questo fatto è dovuto all’effetto della somma operata per ottenere la curva dei contagiati totali al giorno t a partire dai valori misurati giornalmente fino a quello stesso giorno.
Vogliamo ora presentare alcune considerazioni generali sull’uso dei risultati dei test per descrivere l’evoluzione dell’epidemia di Covid-19 e sui criteri per definire i soggetti sui quali effetture il test. Osserviamo che dal 1 marzo fino ai giorni recenti il criterio utilizzato per effettuare il test è legato alla presenza di sintomi tipici di questa malattia. Nel periodo precedente i test venivano effettuati anche a soggetti asintomatici. Esempio in controtendenza è quello del comune di Vo’ Euganeo, dove in Italia è avvenuta la prima morte causata da un’infezione di coronavirus. In quel comune tutta la popolazione è stata sottoposta a test col risultato che circa 7 persone su 10 positive al test erano asintomatiche. Seppure molto rilevante, non ci soffermiamo ora sulla questione della stima del rapporto tra numero effettivo totale di contagiati e quello dei contagiati sintomatici documentati tramite test positivo. Dalle informazioni che ho raccolto, sembra che una nuova fase stia per iniziare a breve o sia da poco iniziata, che prevede la possibilità di effettuare test anche a soggetti asintomatici.
Occupiamoci ora della prima questione. Sia C(t) il numero di nuovi contagiati effettivi relativi al giorno t, ossia il tasso di crescita del totale dei contagiati effettivi. Nell’ipotesi che ci sia un unico tipo di coronavirus attualmente coinvolto, è ragionevole supporre che, indipendentemente dal tempo t, una stessa frazione α sviluppi successivamente i sintomi, mentre la frazione 1 − α rimanga asintomatica o sviluppi i sintomi in maniera lieve, tale da non richiedere l’intervento medico e quindi il test. Individuando tramite il test tutti gli αC(t) individui infettati sintomatici, saremmo quindi in grado di seguire l’evoluzione reale dell’epidemia, a meno di una costante moltiplicativa di poco interesse. Abbiamo qui assunto che il risultato del test non sia affetto da errori e in particolare che tutti gli infetti presentino test positivo, ossia che non ci siano falsi negativi. Comunque, anche in caso contrario non ci sarebbe problema. Infatti degli αC(T) infetti che sviluppano sintomi il valore atteso del numero di positivi al test sarebbe sempre ad ogni tempo pari a αβC(t), con β vicino a 1, mentre 1 − β misura la frazione di falsi negativi.
Naturalmente, uno tra questi individui, infettato al tempo t, viene diagnosticato dopo un tempo successivo τ, che è aleatorio, ma della cui distribuzione abbiamo una stima dai dati raccolti precedentemente. Per ogni test effettuato con esito positivo, possiamo in prima approssimazione andare indietro nel tempo di un numero di giorni pari al valore atteso di τ e aumentare di uno il valore di C a quel tempo. Passato un tempo sufficientemente lungo rispetto al tempo medio tra infezione ed esecuzione del test, avremo una stima di C(t). Possiamo certo commettere errori nell’attribuzione del caso indietro nel tempo perchè per ogni particolare paziente il tempo effettivo tra infezione e diagnosi sarà un po' diverso da quello medio scelto. Per far questo, comunque dobbiamo inoltre avere disponibili i dati disaggregati dei singoli casi diagnosticati. Purtroppo, i dati che abbiamo a disposizione sono aggregati territorialmente. Non possiamo quindi effettuare la procedura descritta. A ogni modo, possiamo scrivere un’equazione (di convoluzione (i non matematici non si spaventino e continuino la lettura)), per la quale possiamo trovare una soluzione approssimata tramite diversi approcci matematici. Se la nostra capacità di effettuare test, copre la richiesta, possiamo quindi in entrambi i casi di dati disaggregati o meno, fornire una risposta al problema di seguire l’evoluzione dell’epidemia utilizzando i risultati dei test.
Ipotizzando di avere la capacità di effettuare test anche ad invividui asintomatici, potremmo ripetere la procedura illustrata in precedenza, per ricostruire la sequenza del numero (1 − α)C(t) di portatori sani, o una ad essa proporzionale. Sia nel caso di un campionamento completamente casuale che nel caso ad esempio di test effettuati sui contatti di un positivo, il valore atteso del numero di positivi risulterebbe sempre poporzionale a C(t), che sommato alla frazione dei sintomatici positivi al test, darebbe sempre una quantità proporzionale a C(t). Naturalmente il numero di test effettuato agli asintomatici non deve variare nel tempo in modo significativo. Allo stesso modo, non possiamo effettuare un’analisi sensata in un intervallo in cui siano presenti due fasi con criteri diversi per individuare i soggetti da sottoporre a test. Questo è il motivo per cui noi eseguiamo l’analisi solo dal 1 marzo.
I test con i tamponi sono stati finora effettuati quasi esclusivamente in base alla richiesta clinica con aumento progressivo dei casi da diagnosticare fino al raggiungimento del picco del tasso di crescita del numero totale di contagiati osservati. Nella fase in cui siamo penso che sarebbe molto importante iniziare una campagna di test su persone asintomatiche. A questo scopo, fissato un obiettivo, per esempio quello di individuare e monitorare le categorie più a rischo di contrarre l’infezione e poi trasmetterla a un elevato numero di altri individui, e.g. personale che opera in strutture sanitarie, ritengo che il contributo degli statistici possa essere molto rilevante per esempio per la scelta qualitativa e quantitativa degli schemi di campionamento ottimali e di conseguenza la formulazione dei criteri per definire le classi di soggetti da sottoporre a test. Inoltre il loro contributo sarebbe importante per la scelta e lo sviluppo dei metodi con le migliori caratteristiche (e.g. efficienza, robustezza, etc.) per effettuare l’analisi statistica dei risultati ed anche per eseguire lo studio teorico di tali metodi. Auspico quindi che la comunità degli statistici venga largamente coinvolta per raggiungere questi obiettivi per perseguire il bene comune.
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche

